- Technik des Alltags
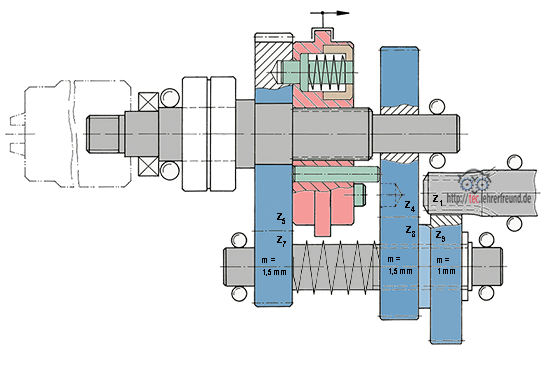
- Maschinenelemente, Funktionsgruppen
- Verbrennungsmotoren
- Werkzeugmaschinen
- Versuche im Unterricht
- Technische Kurven zeichnen
- Schnittdarstellungen im Technischen Zeichnen
- Zeichnungen bemaßen
- Zeichnungs-Normung
- Grundlagen der Technischen Mathematik
- Druck
- Elektrotechnik
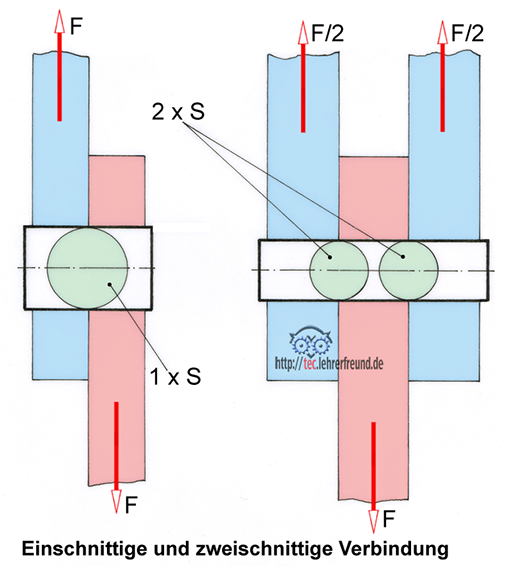
- Festigkeitslehre
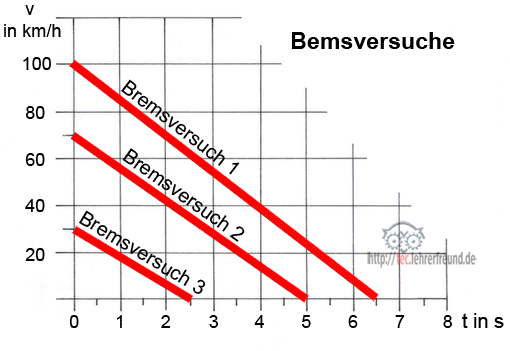
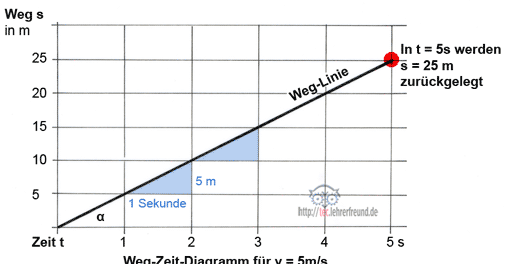
- Geschwindigkeit
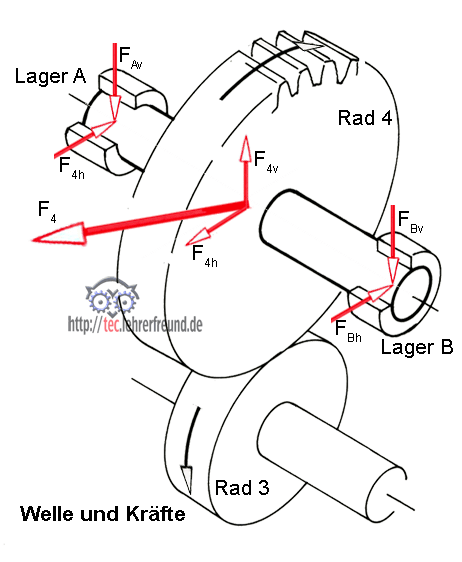
- Kräfte
- Reibung
- Statik
- Frühe Technik
- Baumaschinen
- Elektrik
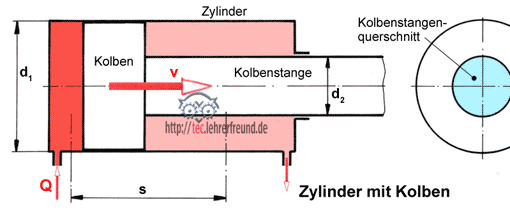
- Hydraulik
- Hydraulische Antriebe
- Kräfte und Drehmomente
- Kupplungen
- Werkstoffe
- Zahnräder
- prima.tec - Technik für Kinder
- Alles …
Geschwindigkeit
Wo sich in der Technik Teile bewegen, lassen sie sich mit den Gesetzen der Geschwindigkeit erschließen. Geschwindigkeiten können geradlinig oder kreisförmig sein.
<Anzeige
Anzeige
Anzeige
Anzeige
> 646 Einträge, 952 Kommentare. Seite generiert in 0.4758 Sekunden bei 142 MySQL-Queries. 84 Lehrer/innen online (3 min Timeout / 1674 ) |