Zahnradberechnung (1) 13.08.2008, 15:51

Zahnradrechnen ist Modulrechnen. Sogar das Bruchrechnen kommt hier zu Ehren.

»So rechnet man‘s«                   

Zahnradberechnungen

Gegenüber Riementrieben haben Zahntriebe einenen großen Vorteil: Sie übertragen Bewegungen und Drehmomente formschlüssig und mit konstant bleibender Übersetzung. Es gibt also keinen Schlupf. Der Schlupf ist das Zurückbleiben der praktischen Drehzahl hinter der theoretischen (berechneten) Drehzahl.  

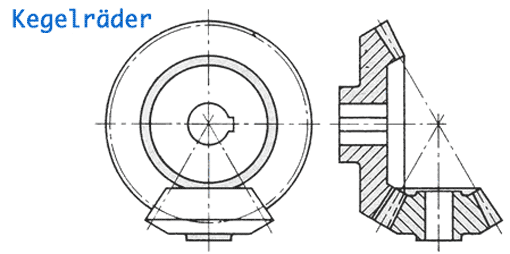
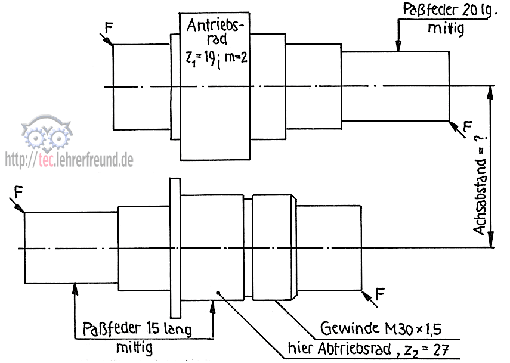
1. Einzelrad im Stirnradtrieb

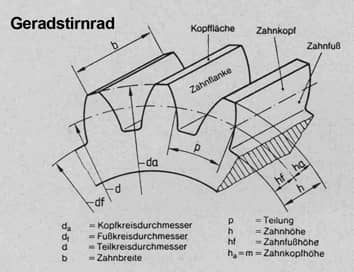
Drei wichtige Größen an einem Zahnrad sind:

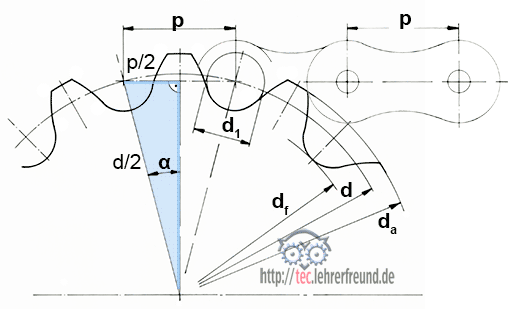
• der Teilkreisdurchmesser d
• die Zähnezahl z
• der Modul m (in mm)

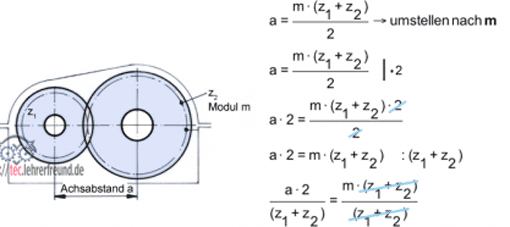
Vielen Zahnradabmessungen liegt der Modul m zugrunde. Er ist in DIN 780 genormt. Zahnräder können nur dann zusammenarbeiten  - man sagt, sie »kämmen« miteinander - wenn ihr Modul gleich groß ist.

Das wichtigste Maß am (Stirn) Zahnrad ist der (theoretische) Teilkreisdurchmesser d.

d = z • m

Der Zahnkopf - er liegt zwischen dem Teilkreisdurchmesser und dem Kopfkreisdurchmesser - ist gleich dem Modul:

h_a = m = 6/6 • m.

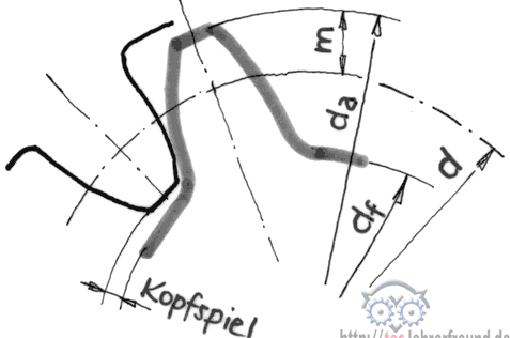
Kräfte werden nur über die Zahnflanken übertragen. Zwischen Fuß und Kopf der beiden Zahnräder muss wegen der Rundungen am Zahnfuß Luft sein, das so genannte Fuß- bzw. Kopfspiel. Das Fuß- oder Kopfspiel ist nach Norm festgelegt mit 1/6 • m. Folglich ist der

Zahnfuß 6/6 • m + 1/6 • m = 7/6 • m hoch.
 

Aus diesen Erkenntnissen kann man die Berechnungsformeln für den Kopfkreisdurchmesser d_a (= Außendurchmesser) und den Fußkreisdurchmesser d_f leicht ableiten:

d_a = d + 2 • m,

d_f = d – 2 • 7/6 • m = m • (z – 7/3)

Ebenso ganz oben : d = z • m

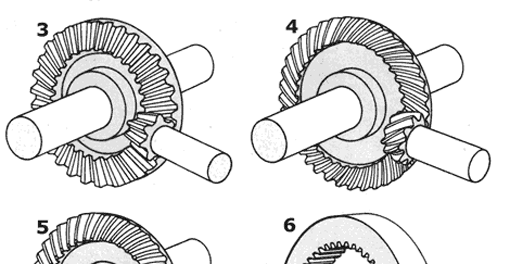
Schrägverzahnte Stirnräder

Bei Zahnrädern mit Schrägverzahnung (Schrägungswinkel β) liegen die »Normalteilung« p_n und der Normalmodul m_n in einer senkrecht zur Verzahnungsrichtung gemessenen Ebene. Die Stirnteilung p_t und der Stirnmodul m_t liegen in Umfangsrichtung und werden an der Stirnfläche gemessen.

Strirnmodul m_t = m_n : cos β

Stirnteilung p_t = p_n : cos β

Bei der Herstellung von Stirnrädern mit Schrägverzahnung entspricht das Profil der Werkzeuge dem Normalprofil. Bei einem kämmenden Zahnradpaar ist ein Zahnrad rechtssteigend und das andere Zahnrad linkssteigend. Der Schrägungswinkel β ist bei beiden Rädern gleich.

__________________

Näheres zu »Formeln umstellen« siehe hier