Statik der Fachwerke (3) 30.01.2013, 04:49
Im tec.LEHRERFREUND-Beitrag »Statik der Fachwerke (1)« wurde die zeichnerische Ermittlung unbekannter Stabkräfte in einem Fachwerk dargestellt. In diesem Beitrag wird überlegt, wie man solche Kräfte rechnerisch bestimmen kann. Das Schnittverfahren nach Ritter hilft weiter.
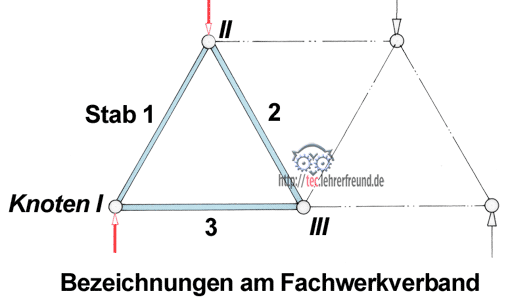
Im tec.LEHRERFREUND-Beitrag »Statik der Fachwerke (1)« wurde dargestellt, wie man unbekannte Stabkräfte in einem Fachwerk zeichnerisch ermittelt. Dort ist mit Bezug auf das Bild unten zu lesen:
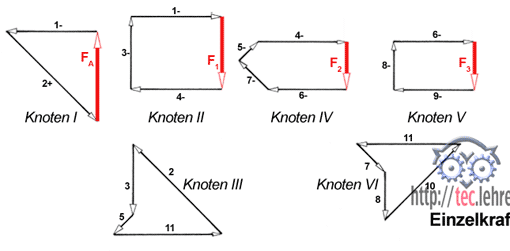
»Zunächst beginnt man an einem Knotenpunkt, an dem nur zwei unbekannte Stabkräfte angreifen, also z. B. mit Knoten I: Wir zeichnen maßstäblich die senkrechte Stützkraft FA. Zusammen mit Stabkraft 1 und Stabkraft 2 ergibt sich ein geschlossenes Krafteck. Die Richtungen der Stabkräfte erhält man durch Parallelverschiebung der Wirklinien aus dem Lageplan in den Kräfteplan. Sehr wichtig ist der Richtungssinn der Stabkräfte: Aus dem Umfahrungssinn des geschlossenen Kraftecks (z. B. für Knoten I) erkennt man, dass Stabkraft 1 nach links, Stabkraft 2 dagegen nach rechts unten gerichtet ist.
Nun überträgt man die Pfeile in den Lageplan unmittelbar neben den betrachteten Knoten, weil sich der Richtungssinn der Stabkräfte immer auf den Knoten bezieht. Damit wird klar gestellt, ob es sich um einen Zugstab oder um einen Druckstab handelt. Es gilt: Ein zum Knoten weisender Pfeil bedeutet Druck auf den Knoten, es liegt also ein Druckstab vor (Stab l); andernfalls ist der Stab (wie Stab 2) ein Zugstab.«
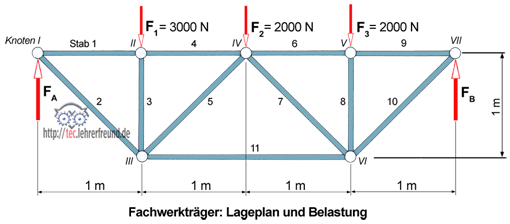
Daran anknüpfend soll in diesem Beitrag überlegt werden, wie man solche Kräfte rechnerisch bestimmen kann. Hier hilft uns das Schnittverfahren nach Ritter weiter. Es geht von der Erkenntnis aus, dass an jedem Knoten die Momentensumme gleich Null ist. Auch darf in dem betrachteten System nur eine Unbekannte vorhanden sein.
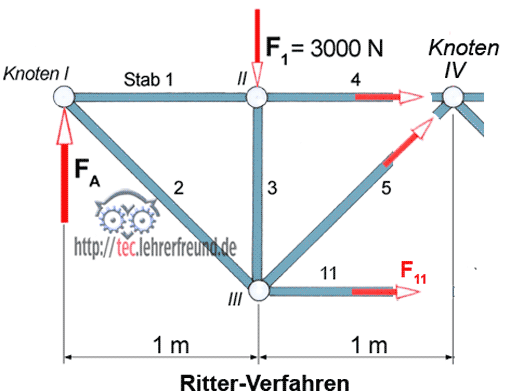
Aufgabe 1: Man will die Belastung des Stabs 11 berechnen. So geht man vor:
- Man schneidet das Fachwerk an den Stäben 4, 5 und 11 durch.
- Man wählt als Momentendrehpunkt einen Knoten aus, auf den Stab 11 ein Drehmoment ausübt. Das ist nur Knoten IV; die Kräfte in den Stäben 4 und 5 gehen durch den Knoten, üben also - weil sie keine wirksamen Hebelarme besitzen - keine Momente aus.
Es spielt dabei keine Rolle, dass der Drehpunkt außerhalb des geschnittenen Teils liegt.
Die Stützkraft FA haben wir im Beitrag »Statik der Fachwerke (1)« mit 3750 N ermittelt.
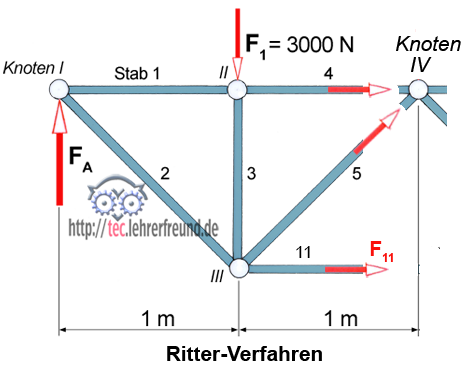
Momentengleichung:
Σ M(IV) = 0 = F11 • 1m + F1 • 1m – FA • 2 m
F11 = (FA • 2 m – F1 • 1m) : 1 m = (3750 N • 2 m – 3000 N • 1 m) : 1 m
F11 = 4 500 N
Aufgabe 2:
Man will die Belastung des Stabs 4 berechnen: Man legt den Drehpunkt in den Knoten III. Dort ergeben die Stäbe 2, 3 und 5 keine Drehmomente.
Momentengleichung:
Σ M(III) = 0 = F4 • 1m + FA • 1m
F4 = FA • 1 m : 1 m = 3750 N • 1m : 1m = 3 750 N
Wird das Zahlenergebnis einer solchen Berechnung negativ, dann heißt das nur, dass die Richtung der Stabkraft falsch angenommen war, also anstatt z.B. eine Zugkraft eine Druckkraft eingesetzt wurde. Die anderen äußeren Kräfte (hier FA und F1) müssen allerdings richtig eingesetzt werden.