Eine Sinuskurve konstruieren 04.01.2009, 20:48
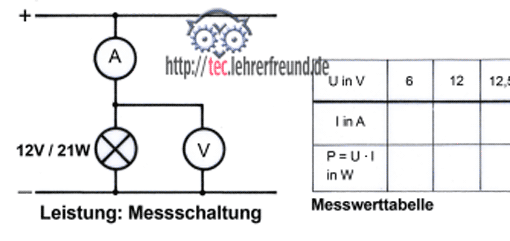
Die Winkelfunktionen Sinus, Cosinus, Tangens und Cotangens gehen auf den Kreis zurück. In der Technik hat die Sinuskurve eine wichtige Bedeutung bei Drehbewegungen: Drehung des Rotors im Generator, der Kurbelwelle im Verbrennungsmotor, für den Gleichförmigkeitsgrad einer Gelenkwelle usw.
Eine Sinuslinie konstruieren
Die Winkelfunktionen Sinus, Cosinus, Tangens und Cotangens gehen auf einen Kreis zurück. In der Technik stößt man regelmäßig auf sie bei Drehbewegungen: Drehung des Rotors im Generator, der Kurbelwelle im Verbrennungsmotor, beim Gleichförmigkeitsgrad einer Gelenkwelle, usw.
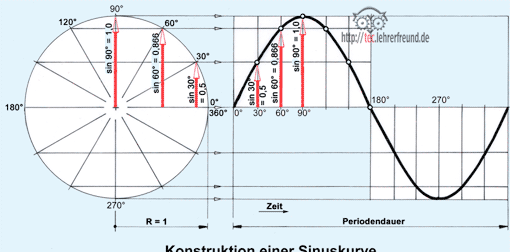
Im so genannten Einheitskreis mit dem Radius R = 1 (z. B. 1 mm, 1 cm, 1 dm, 1 m usw.) lässt sich die Größe des sin α als senkrechte Strecke - sie ist für drei Winkelwerte mit roten Pfeilen dargestellt - herausmessen. Ist R = 1 m, dann ist z. B. der Sinus des Winkels 60° = 0,866 m. Ihren höchsten Wert erreicht die Sinusfunktion mit 1,0 bei α = 90°, den kleinsten mit Null bei α = 0°.
Den Verlauf einer Sinuslinie konstruiert man in folgenden Schritten:
1. Linke Kreisansicht in 12 (24) Segmente einteilen; diese am Umfang nummerieren: 0°, 30°, 60°, 90°, 120 ° usw. bis 360°
2. Rechte Ansicht ebenfalls in 12 (24) gleich breite Streifen einteilen und nummerieren von 0° bis 360°
3. Die Durchstoßpunkte der Sektorstrahlen in der Kreisansicht in die Seitenansicht projizieren
4. Die einander entsprechenden Schnittpunkte in der rechten Ansicht mit einem Kurvenlineal verbinden.
Je schmaler die Streifen in der rechten Ansicht sind (sie entsprechen dann einer höheren Drehzahl), desto enger wird die Kurve. Zeichnet man mehr Kurvenäste als die beiden hier dargestellten, dann wiederholen sie sich nach jeder Umdrehung, d. h. nach Erreichen von 360°.
Übung
Drucken Sie die vergrößerte Version der folgenden Zeichnung aus und konstruieren Sie die Sinuslinie.
Lösung