Laufkran: Statik, Kräfte 24.02.2012, 13:58

Die Laufkatze ist die Baugruppe bei Laufkranen, die die Hubeinrichtung trägt. An einem praktischen Beispiel rechnen wir die Motorleistung, die Belastung des Katzrahmens und das Bremssystem durch.

Beachten: Niveau Techn. Gymnasium, Berufskolleg u. Ä. 

Laufkran

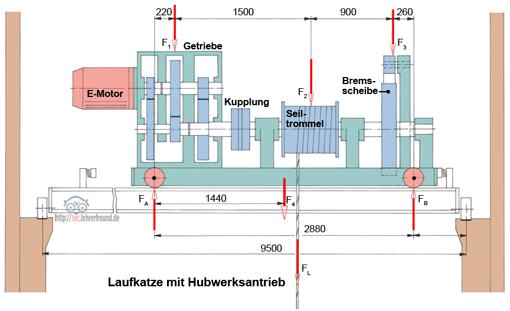
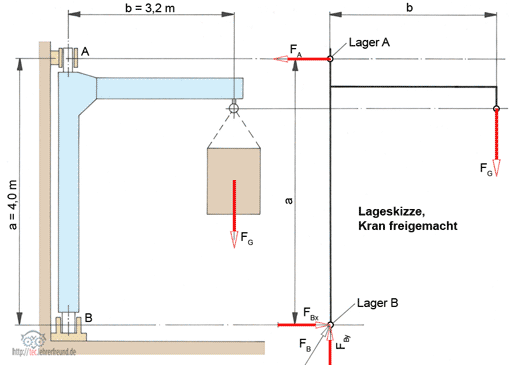
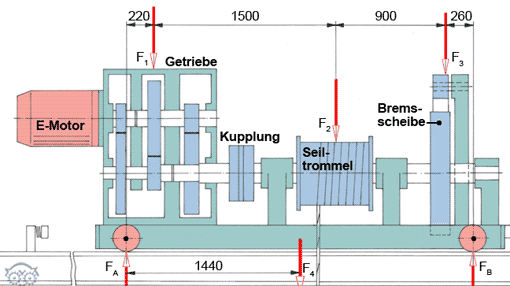
Das Bild zeigt die stark vereinfachte Konstruktion eines Laufkrans, wie sie in Werkstätten und Fabrikhallen eingesetzt werden. Laufkrane bewegen sich auf den Schienen einer Hochbahn und lassen damit Arbeitsflächen am Boden frei. Der farbig dargestellte Teil des Krans ist die quer laufende Laufkatze mit Hubwerksantrieb, deren Kernbaugruppe eine Seilwinde ist. Sie wird von einem E-Motor über ein dreistufiges Getriebe angetrieben. 

Gegeben sind:
Motorleistung P_M = 17,5 kW; n_M = 720 1/min
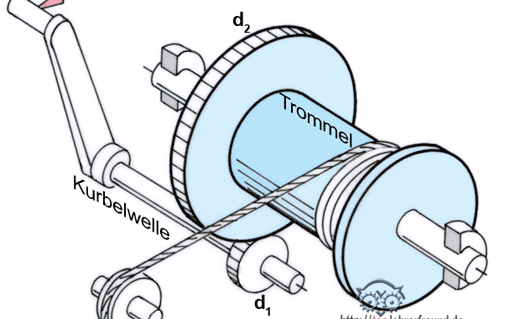
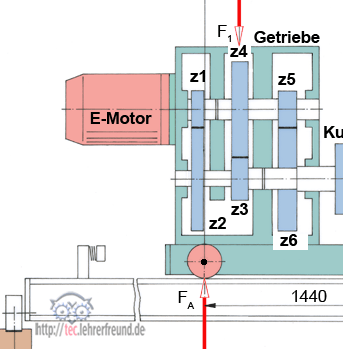
Getriebe:
z₁ =  23
z₂ =  70
z₃ =  19
z₄ =  43
z₅ =  19
z₆ =  43 

Wirkungsgrad η_G = 0,78

Seiltrommel:
Trommeldurchmesser d_Tr = 260 mm
Last max. F_L = 18 kN 
η_Tr = 0,92

Aufgaben

1. Motorleistung

a) In der Getriebezeichnung sind die Zahnräder zu benennen ( z₁, z₂, usw.)  
b) Das Gesamtübersetzungsverhältnis des Getriebes ist zu berechnen.

c) Der Seiltrommel-Antrieb soll 10% mehr Drehmoment aufnehmen können als am Hubseil bei F_{L max} verlangt wird. Rechnen Sie nach, ob diese Bedingung eingehalten wird.

2. Belastung der Laufkatze 

Die Hubeinrichtung steht auf zwei Trägern. Die folgenden Lastangaben beziehen sich auf einen Träger.
In F₁ = 5 500 N sind die anteiligen Gewichte von Motor, Getriebe und Kupplung zusammengefasst.
In F₂ = 12 500 N ist das Seiltrommelgewicht mit der Last F_L zusammengefasst.
F₃ = 1 200 N ist das Gewicht der Bremseinrichtung.
F₄ = 3 000 N ist das Eigengewicht des Laufkatzenrahmens.

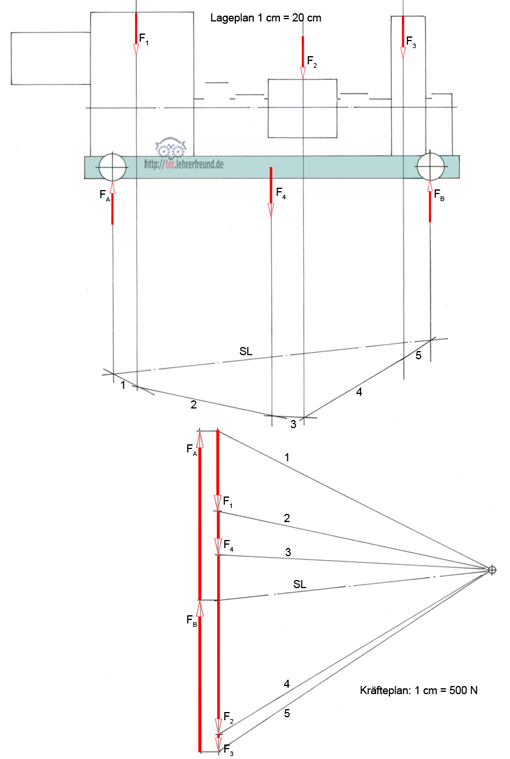
Die Lagerkräfte F_A und F_B (für einen Träger) sind zeichnerisch zu bestimmen.

3. Bremseinrichtung 

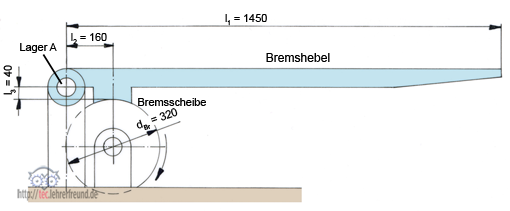
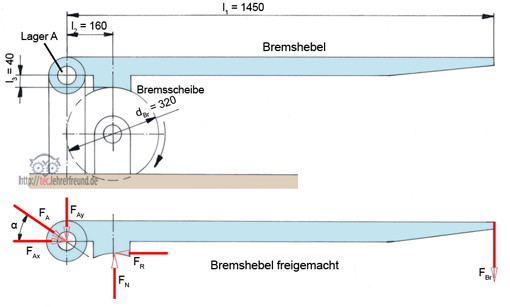
Der Bremshebel soll an der Scheibe mit dem Durchmesser 320 mm ein Bremsmoment von 2,5 kNm abbremsen. Die Reibzahl zwischen Bremsbelag und Bremsscheibe ist 0,45.

a) Der Bremshebel ist freizumachen 
b) Zu berechnen sind die Reibkraft F_R und die Normalkraft F_N.
c) Zu berechnen sind die Bremskraft F_Br und die Lagerkraft F_A. 

Lösungsvorschläge 

1. Motorleistung

a) Zahnräder: siehe Skizze

b) i _ges = (z₂ ∙ z₄ ∙ z₆) : (z₁ ∙ z₃ ∙ z₅)
= 70 ∙ 43 ∙ 43) : (23 ∙ 19 ∙ 19)

i_ges = 15,588 

c) Vom Motor kommen an der Seilwinde an:
M_Tr1 = M_M ∙ i_ges ∙ η_ges =
= (9550 ∙ 17,5 : 720) ∙ (i_ges ∙ η_ges)
M_Tr1 = 2 596,5 Nm

Unter F_L = 18 000 N nimmt die Seiltrommel auf:
M_Tr2 = F_L ∙ d_Tr/2 = 8 000 N ∙ 0,26 m / 2 =
M_Tr2 = 2 340 Nm

M_Tr1 : M_Tr2 = 2 596,5 Nm : 2 340 Nm = 1,11, d. h.  der Motorantrieb liefert ein Drehmoment, das 11 % höher ist als das an der Seiltrommel verlangte.

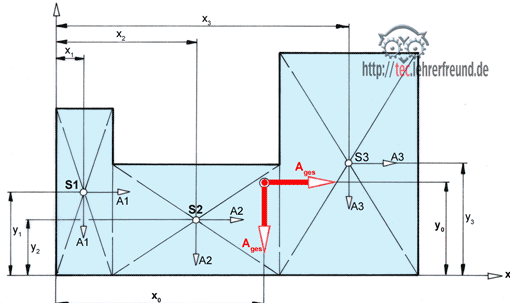
2. Belastung der Laufkatze: siehe Skizze

Kräfte über Seileck ermittelt; herausgemessen: 

F_A = 11 650 N 
F_B = 10 550 N

3. Bremse (siehe Skizze) 

a) Bremshebel freigemacht

b) Reibkraft F_R
F_R = M_R ∙ 2 : d_Br =  2500 Nm ∙ 2 : 0,32 m
F_R = 15 625 N

Normalkraft F_N
F_N = F_R : μ = 15 625 N : 0,45 =
F_N = 34 722,2 N

c) Bremskraft F_Br
ΣM_(A) = 0 = F_Br ∙ l₁ + F_R ∙ l₃  - F_N ∙ l₂
F_Br . l₁ = F_N ∙ l₂ - F_R ∙ l₃
F_Br = (F_N ∙ l₂ - F_R ∙ l₃) : l₁
F_Br = 3 400,4 N

ΣF_x = 0 = F_Ax - F_R   –>   F_Ax = F_R = 15 625 N
ΣF_y = 0 = F_N - F_Ay - F_Br   –>   F_Ay = F_N - F_Br
F_Ay = 34 722,2 N - 3 400,4 N
F_Ay = 31 321,8 N

F_A = √F_Ax² + F_Ay² =  √(15 625 N)² + (31 321,8 N)²

F_A = 35 002,8 N

tan α = F_Ay : F_Ax = 31 321,8 N : 15 625 N = 2,005
α = 63,5°

___________________________

Die unvollständige Skizze unten ist für die Verwendung in Arbeitsblättern gedacht.