Korkenzieher 19.02.2012, 11:03

Das Problem, Korken aus der Flasche zu ziehen, hat unzählige Tüftler angeregt, Korkenzieher zu erfinden. Entsprechend viele Konstruktionen - gute und weniger überzeugende - liegen in unseren Schubladen. Wir greifen hier zwei von der anspruchsvolleren Sorte heraus: den Flügel-Korkenzieher und den Scheren-Korkenzieher.

Korkenzieher

Zu den kleinen technischen Wunderwerken, die wir jeden Tag im Haushalt verwenden, zählt der Korkenzieher. Die Schweizer nennen ihn Zapfenzieher, die Österreicher Stoppelzieher.  
Das Problem, Korken aus der Flasche zu ziehen, hat unzählige Tüftler angeregt, Lösungen zu finden. Entsprechend viele Konstruktionen - gute und weniger überzeugende - finden wir in unseren Schubladen. Sammlern verdanken wir, dass die Vielfalt nicht verloren ging. Von diesem unglaublichen Erfinderfleiß kann man sich beispielsweise im Kaiserstühler Korkenziehermuseum in Burkheim überzeugen. 

Wir greifen hier zwei Korkenziehermodelle heraus: den Flügel-Korkenzieher und den Scheren-Korkenzieher. Weintrinker hier und dort haben den beiden Konstruktionen sicher noch andere Bezeichnungen verpasst.
Wir betrachten die Konstruktionen auch aus mathematischer und wirtschaftlicher Sicht und wollen herausfinden, welcher der beiden der wirksamere ist.

Flügel-Korkenzieher
Aufbau und Funktion
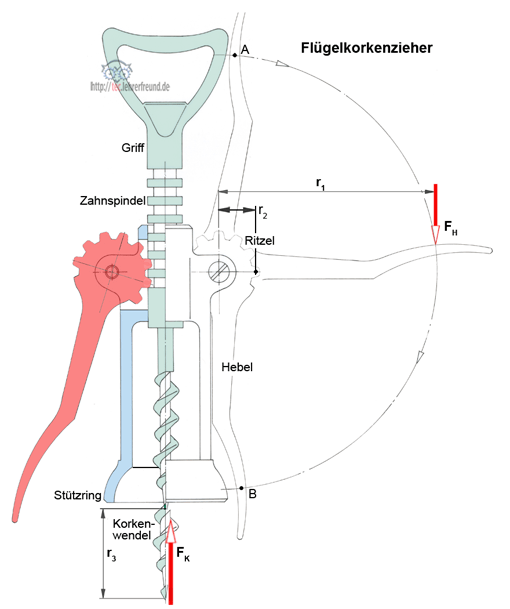
Das tragende Teil ist ein Gussgehäuse, in dessen zentraler Bohrung die an den Griff anschließende Zahnspindel mit der Korkenwendel sich axial verschieben und drehen lässt. Dazu kommen zwei flügelförmige Hebel mit Schrauben als Drehachse und Befestigung. Die Schrauben sind an ihren Gewindeenden vernietet.
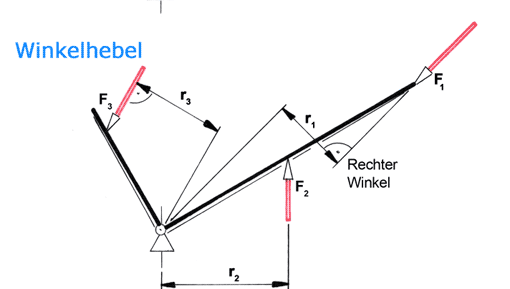
Vor dem Eindrehen in den Kork liegen die Hebel am Gehäuse an. Beim Eindrehen steigen sie, von der Zahnspindel über das Ritzel mitgenommen, von B nach A auf dem Radius r₁ nach oben.
Der Kork wird herausgezogen, indem man die beiden Hebel von A nach B drückt. Die dafür aufgewendete Kraft F_H ist - und das macht den Komfort des Flügel-Korkenziehers aus - wesentlich kleiner als die Kraft, mit der der Flaschenhals den Korken festhält. Die Kraftersparnis hat mit dem Hebelübersetzungsverhältnis i = r₁ : r₂ zu tun. Bei dem hier dargestellten Flügel-Korkenzieher liegt i bei etwa 78 mm : 12 mm = 6,5 : 1.

Für die Berechnung der Kräfte wählen wir den Ansatz über die Arbeitsformel: Hineingesteckte Arbeit A₁ =  herausgeholte Arbeit A₂, also A₁ = A₂. (Wir lassen außer Acht, dass gegen Ende des Herausziehens der Korkenwiderstand abnimmt).

Die Hebelarbeit A₁ wird an zwei Hebeln verrichtet. An einem Hebel ist es F_H mal dem Hebelweg. Der Hebelweg ist der halbe Umfang des Kreises r₁.

A₁ = 2 • (F_H • s); s ist angenähert r₁ • π:
A₁ = 2 • F_H • r₁ • π

Die herausgeholte Arbeit A₂ ergibt sich aus dem Korkenwiderstand und dem Korkenweg r₃:
A₂ = F_K • r₃

A₁ = A₂ lässt sich also schreiben:

2 • F_H • r₁ • π = F_K • r₃ –>
F_H = (F_K • r₃) : (2 • r₁ • π)

Beispiel: Wenn der Korken dem Herausziehen einen Widerstand F_K = 60 daN = 600 N entgegensetzt, welche Handkraft F_H ist dann erforderlich?
F_H = (F_K • r₃) : (2 • r₁ • π)
F_H = (600 N • 12 mm) : (2 • 78 mm • π)
F_H = 14,7 N

Dass der Flügel-Korkenzieher besonders häufig anzutreffen ist, ist gewiss ein Hinweis darauf, dass er eine gute und bewährte Konstruktion sein muss. 
Wollen wir den Aufwand bei der Herstellung des Geräts abschätzen, dann zählen wir seine Einzelteile: Es sind 7 Stück. 

Scherenkorkenzieher
Bei dieser höchst interessanten Erfindung sieht die Bauteile-Bilanz leider wesentlich schlechter aus. Hier zählen wir 30 Teile. Genau genommen sitzt auf jedem Gelenkbolzen nochmal eine Scheibe, so dass sich 43 Teile ergeben. Die 13 Gelenkstellen sind mit Sicherheit höchst schädlich für den Wirkungsgrad. Ein Trost: Im Griff ist eine Feder untergebracht, die so auf die beiden oberen Glieder drückt, dass die Schere nach Loslassen des Griffs auf Minimallänge zusammengeschoben wird.
Der Scheren-Korkenzieher scheint auf ein sehr altes französisches Patent zurückzugehen. Die Herstellerfirma hat ihrem Produkt den netten Namen Zig Zag  gegeben (was sie in Frankreich wie »le sig-sag« aussprechen). Überhaupt kann man immer wieder feststellen, dass die Franzosen pfiffige und intelligente Erfinder sind. Dies beweisen nicht nur Weg weisende Erzeugnisse in der Automobil- und Flugzeugtechnik.
Im Fall des Scheren-Korkenziehers ist das auch so, nur zeigt schon die Bauteilzählung, dass der Korkenzieher betriebswirtschaftlich gesehen ein hoffnungsloser Fall ist. Comme c'est dommage!

Auch hier setzen wir die Arbeitsgleichung ein:
A₁       =    A₂
F_H • l₁ = F_K • l₂ –>
F_H = F_K • l₂ : l₁
Um einen Korkenwiderstand von 600 N zu überwinden, ergibt sich eine Zugkraft
F_H = 600 N • 34 mm : 160 mm =
F_H = 127,5 N.

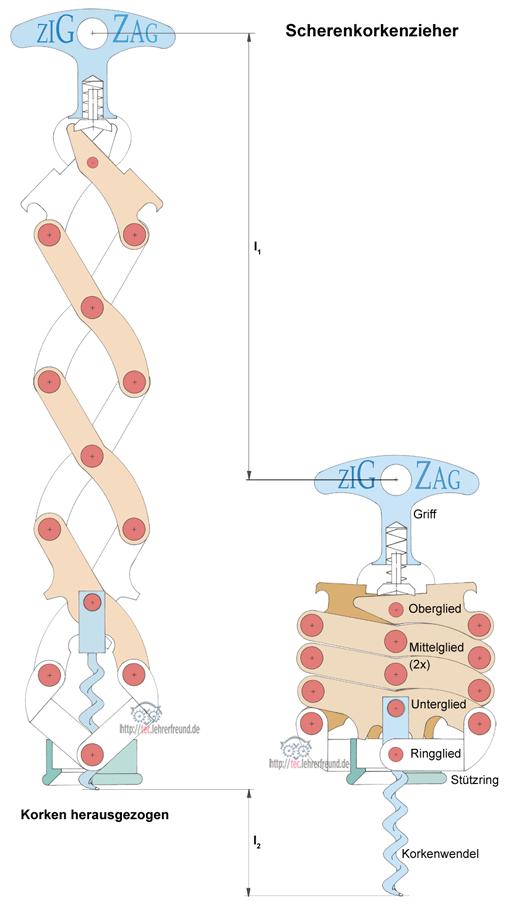
Erkenntnis: Der Scherenkorkenzieher verlangt fast 8 Mal mehr Zugkraft als sein modernerer Kollege, der Flügelkorkenzieher. Wir wollen ihm zugute halten, dass der vorteilhaftere Flügelkorkenzieher noch nicht erfunden war, als sein älterer Bruder Weinflaschen entkorkte. 

Zur Geometrie der Korkenzieherschere

a) Warum kann man die Schere nicht auf Null zusammendrücken?

b) Warum macht die Korkenwendel beim Auseinanderziehen der Schere einen kleineren Weg als der Griff? 

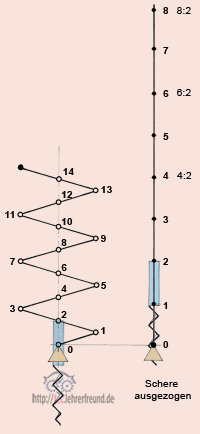
Zu a)
Die Schere kann man mit einer Druckfeder vergleichen. Wenn man eine 100 mm lange Druckfeder aus 2-mm-Draht mit 20 Windungen zusammendrückt, ist bei 60 mm Schluss: Die Feder bildet jetzt einen 2 x 20 = 40 mm langen Federblock, bei dem die Windungen satt aufeinander sitzen.
So ist es auch beim Scherenkorkenzieher. Seine Blockhöhe ist umso größer, je breiter die Scherenglieder sind.

Zu b)
Siehe Skizzen oben:
Die Korkenwendel mit ihrer Einhängegabel hängt immer am Gelenk 2. Bei der einfachsten Schere (Zugpunkt 4) ergibt sich ein Übersetzungsverhältnis i = 4 : 2 = 2 : 1, d. h. bei 2 cm Griffweg macht die Korkenwendel nur 1 cm Weg. Bei der zweigliedrigen Schere (Zugpunkt 6) ist i = 6 : 2 = 3 : 1, bei der dreigliedrigen 8 : 2 = 4 : 1 usw.

_____________________________________________________

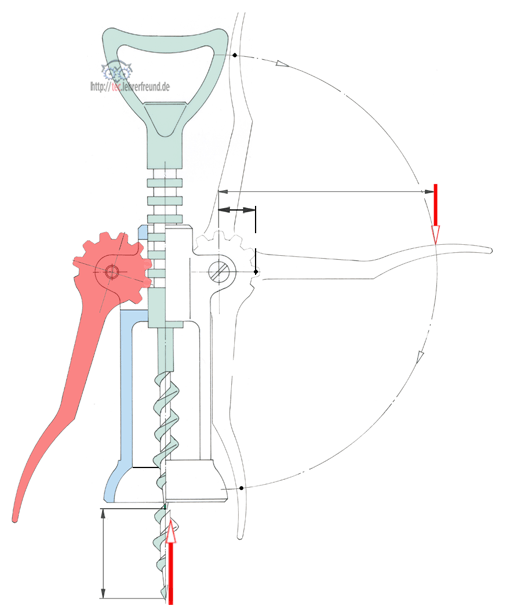
Die Skizze unten ist für die Verwendung in Arbeitsblättern gedacht