Getriebewelle berechnen 16.10.2015, 06:01

Wie berechnet man in einem Zahnradgetriebe die an Zahnrädern und Wellen angreifenden Kräfte und Drehmomente?

Getriebewelle berechnen 

Im tec.LEHRERFREUND-Beitrag »Lernprojekt Zweigang-Getriebe« ist eine Getriebewelle zu berechnen. Im vorliegenden Beitrag bereiten wir die Aufgabe vor. 

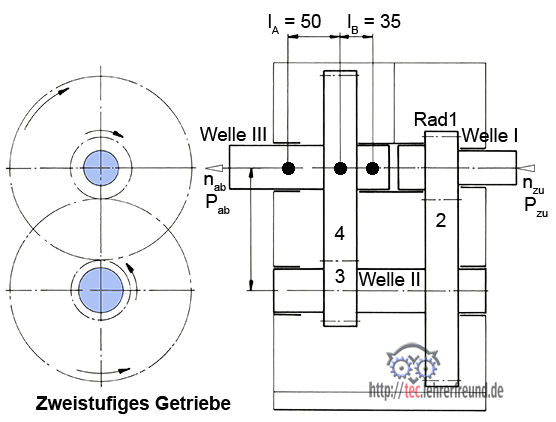
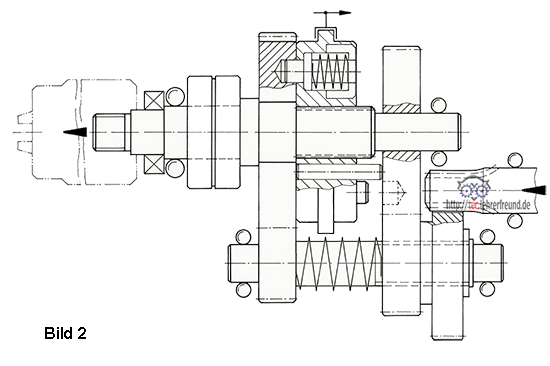
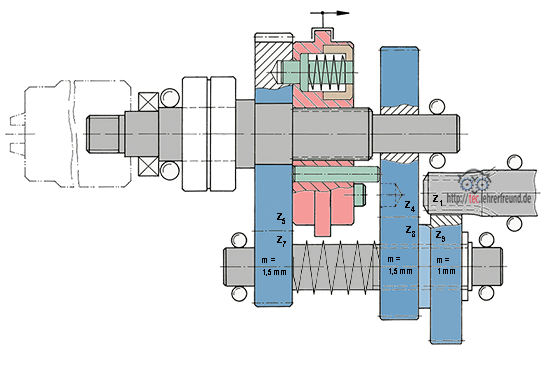
Das skizzierte zweistufige, nicht schaltbare Getriebe wird mit n_zu = 750 1/min angetrieben; es nimmt P_zu = 2,5 kW auf. Die Zahnräder sind geradeverzahnt mit 20° Eingriffswinkel; ihr Modul ist 2,0 mm.  

Die Zähnezahlen sind: 
z₁ = 31
z₂ = 80 
z₃ = 29
z₄ = 86 
Die dazugehörigen Teilkreisdurchmesser sind 
d₁ = z₁ • m = 31 • 2,0 mm = 62 mm; 
d₂ = 160; 
d₃ = 58; 
d₄ = 172 
Die Übersetzungen im Getriebe sind: 
i_1-2 = z₂ : z₁ = 80 : 31 = 2,581
i_3-4 = z₄ : z₃ = 86 : 29 = 2,966
i_ges = (z₂ : z₁) • (z₄ : z₃) = 7,653  

Aufgabe 
Wir berechnen die von der Abtriebswelle III übertragenen Kräfte (auch Lagerkräfte), Drehzahl und Drehmomente. 

Das an Welle I wirkende Drehmoment M_I lässt sich aus der Drehzahl n₁ (n_zu) und der Leistung P₁ (P_zu) berechnen:
Aus P₁ = M_I • n₁ : 9550 ergibt sich  
M_I = P₁ • 9550 : n₁ = 2,5 • 9550 : 750 = 31,833 Nm 

M_II = M_I • i_1-2 = 31,833 Nm • 2,581 = 82,162 Nm
M_III = M_II • i_3-4 = 82,162 Nm • 2,996 = 246,157 Nm 

n_ab = n_zu : ig_es = 750 1/min : 7,653 =
n_ab = 98,1 1/min

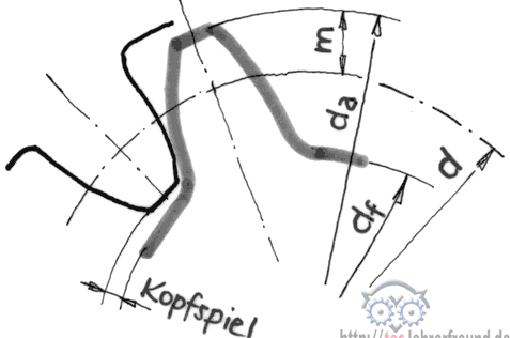
Daraus berechnen wir die am Zahnrad 4 wirkende Umfangskraft (Skizze a))

MIII = F_U4 • d4 / 2 ––>
F_U4 = 2 • M_III/ d₄  = 2 • 246,157 Nm / 0,172 m 

F_U4 = 2 862 N  

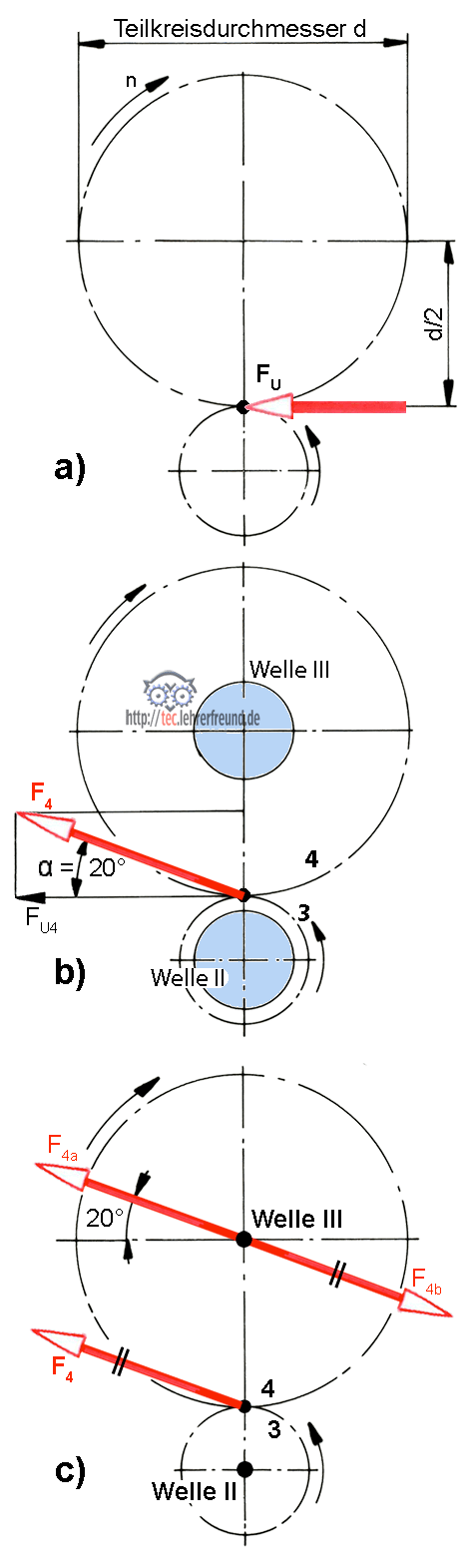
F_U4 ist die horizontale Komponente der Kraft F₄, die in Richtung der unter 20° liegenden Eingriffslinie wirkt (Skizze b)). 

Eingrifflinie (Skizze): 

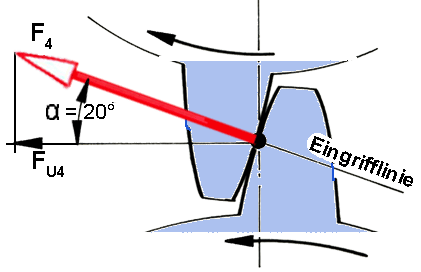
Der Berührungspunkt zweier Zahnflanken bewegt sich während des gesamten Eingriffs auf einer Geraden, der Eingriffslinie. Den Winkel, um den die Eingriffslinie geneigt ist, nennt man Eingriffswinkel; er beträgt üblicherweise 20°. 
Sehr gute Erläuterungen dazu finden Sie hier.

Anmerkung zur Formel P₁ = M_I • n₁ : 9550 
Die Formel ist als Zahlenwertgleichung geschrieben. Bei der Verwendung solcher Gleichungen werden keine Einheiten eingesetzt; man muss sich einfach strikt an die im Tabellenbuch oder in sonst einem Formelwerk angegebenen Maßeinheiten halten. In der vorliegenden Formel sind dies:
- Leistung P in kW
- Drehzahl n in 1/min und
- Drehmoment M in Nm 
In der Umrechnungszahl 9550 sind mehrere Einzel-Umrechnungszahlen zusammengefasst, die wir hier nicht im Einzelnen besprechen wollen. Würde man zu einer Berechnung mit P = M • n : 9550 nur die Einheiten für M und n schreiben, ergäbe sich eine Leistung mit der (falschen) Einheit Nm/min (anstatt kW). Genau dies ist die Aufgabe des Faktors 9550: Er bewerkstelligt den Ausgleich für die fehlenden Einheiten. 
 

Skizze b), nicht maßstäblich
F₄ = F_U4 : cos α = 2 862 N : 0,94 = 
F₄ = 3 045 N 

Welche Kräfte beanspruchen die Welle III? 

Man erkennt es besser, wenn man F₄ zwei Mal als F_4a und F_4b hinzufügt (Skizze c)). Dadurch wird an der Kraftwirkung nichts verändert, denn die beiden Kräfte heben sich gegenseitig auf. F₄ und F_4b ergeben ein Kräftepaar, das die Welle III verdreht; F_4a wirkt in Wellenmitte und übt eine Biegekraft auf die Welle aus. F_4a erzeugt auch die Lagerkräfte F_A und F_B. 

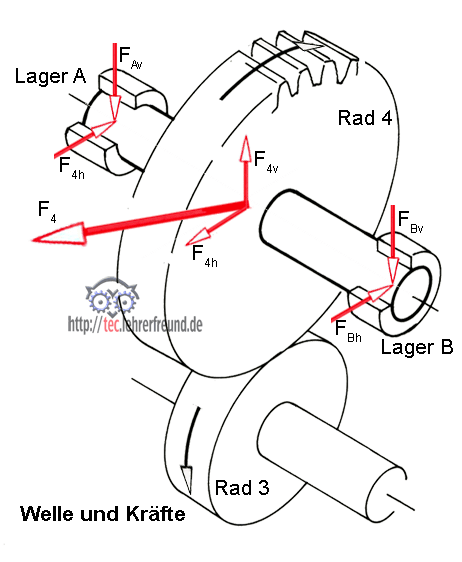
Aus der Skizze »Welle und Kräfte« berechnen wir die sich aus F₄ ergebenden waagrechten und senkrechten Komponenten. 

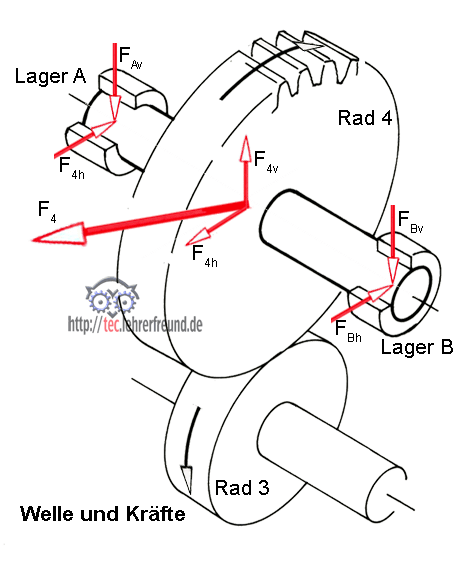
F_4h = F₄ • cos α = 3 045 N • 0,94 =  
F_4h = 2 862 N 

F₄ • sin α = 3 045 N • 0,342 =  
F_4v = 1 041 N 

Lagerkräfte F_A und F_B

Waagrechte Komponenten 

ΣM(B) = 0 = F_Ah • (l_A + l_B) – F_4h • l_B ; F_4h = 2 862 N 

F_Ah = F_4h • l_B : (l_A + l_B) = 2 862 N • 35 mm : 85 mm = 

F_Ah = 1104 N

ΣF_x = 0 = F_Ah – F_4h + F_Bh ––> F_Bh = F_4h – F_Ah = 2 862 N – 1 178 N

F_Bh = 1 684 N

Senkrechte Komponenten 

ΣM(B) = 0 = F_4v • l_B – F_Av • (l_A + l_B) = 1 041 N • 35 mm – F_Av • 85 mm 

F_Av = 429 N

ΣF_y = 0 = F_4v – F_Av – F_Bv

F_Bv = F_4v – F_Av = 1 041 N – 429 N = 

F_Bv = 612 N