Geometrische Grundkonstruktionen (2) 19.11.2013, 08:01
Geometrisch konstruieren heißt, eine vorgegebene Figur mit Zirkel und Lineal exakt darzustellen. In diesem Beitrag wird dies am Beispiel von Kreisanschlüssen gezeigt.
Geometrische Grundkonstruktionen (2)
Geometrisch konstruieren heißt, eine vorgegebene Figur mit Zirkel und Lineal exakt darzustellen. Weil dies aber recht zeitaufwendig sein kann, ist es in der Praxis sicher nicht immer ein Sündenfall, wenn man sich mit Erleichterungen behilft. Eine der Erleichterungen ist das Zeichendreieck mit einer Gradeinteilung. Auf diese Weise ist das Zeichnen von rechten Winkeln gängige Praxis.
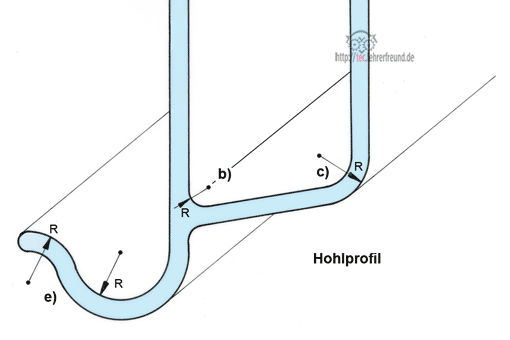
Das unten dargestellte Hohlprofil hat Formen, an denen wir die Darstellung wichtiger Grundkonstruktionen erläutern wollen. Die Grundkonstruktionen sind anschließend mit a), b), c), d) und e) gekennzeichnet.
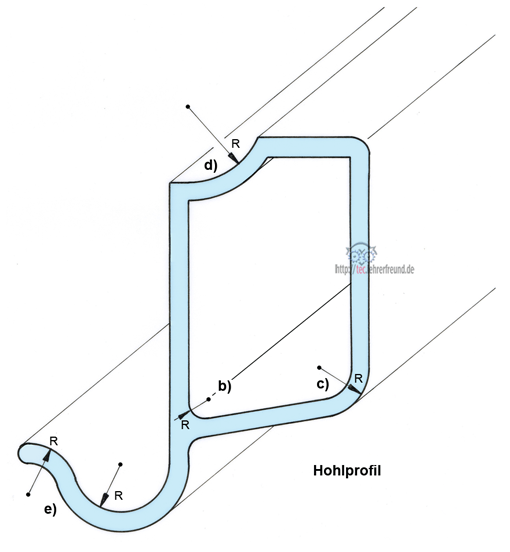
Geometrisch konstruieren heißt, eine vorgegebene Figur mit Zirkel und Lineal exakt darzustellen. In diesem Beitrag wird dies am Beispiel von Kreisanschlüssen gezeigt. Dabei nehmen wir uns bei jeder Aufgabe vor, als Erstes die Anschlusspunkte zu konstruieren. Danach wird der Kreisbogen eingezeichnet. (In Aufgabe d) sind die Anschlusspunkte bereits gegeben).
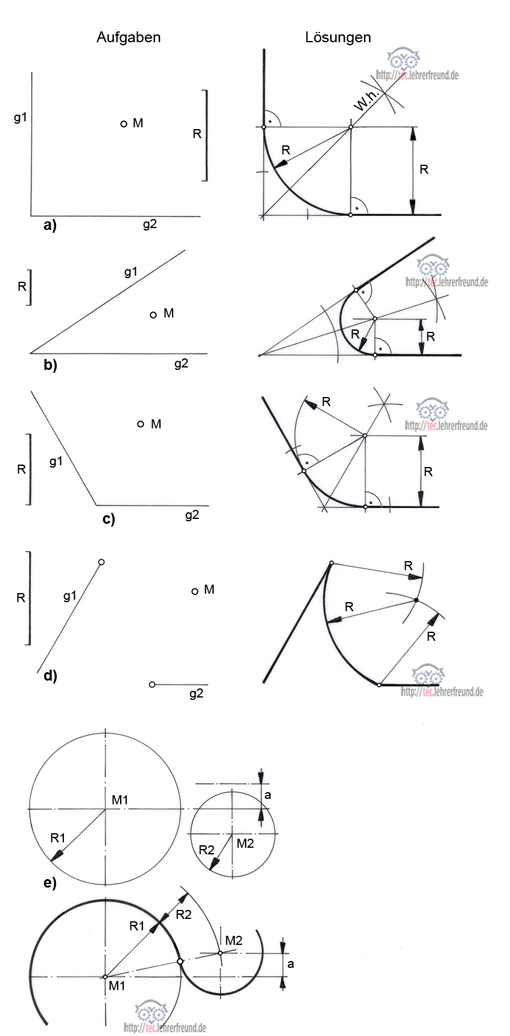
Aufgabe a) Gegeben sind die rechtwinklig zueinander liegenden Geraden g1 und g2. Sie sollen mit dem Radius R verbunden werden.
Lösung: Die Mitte M muss sowohl von g1 als auch von g2 den Abstand R besitzen. Dies ist auf Parallelen zu g1 und g2 der Fall, die von den Geraden den Abstand R haben. Zwei Möglichkeiten:
– Wir ziehen diese Parallelen und erhalten den Schnittpunkt M.
– Wir konstruieren die Winkelhalbierende W.h. und bringen sie mit einer der Parallelen zum Schnitt in M.
Die Anschlusspunkte sind die Schnittpunkte zwischen den Geraden g1 und g2 und den Parallelen. Sie bilden die Tangenten zu dem nun zu ziehenden Kreisbogen.
Aufgabe b) Gegeben sind die in einem spitzen Winkel zueinander liegenden Geraden g1 und g2. Sie sollen mit dem Radius R verbunden werden.
Lösung: Die Mitte M muss sowohl von g1 als auch von g2 den Abstand R besitzen. Dies ist auf Parallelen zu g1 und g2 der Fall, die von den Geraden den Abstand R haben. Zwei Möglichkeiten:
– Wir konstruieren die Winkelhalbierende W.h. und bringen sie mit einer der Parallelen zum Schnitt in M.
– Lösung 2 ist nicht dargestellt. Wir ziehen die Parallelen im Abstand R zu den Geradenund erhalten den Schnittpunkt M.
Die Anschlusspunkte sind die Schnittpunkte, die sich ergeben, wenn man durch M senkrecht zu g1 und g2 verlaufenden Linien zeichnet. g1 und g2 bilden die Tangenten zu dem nun zu ziehenden Kreisbogen.
Aufgabe c) Gegeben sind die in einem stumpfen Winkel zueinander liegenden Geraden g1 und g2. Sie sollen mit dem Radius R verbunden werden.
Lösung: Wie in Aufgabe b).
Aufgabe d) Zwei Geraden g1 und g2, deren Schnittpunkt außerhalb des Zeichenblatts liegt, sollen von zwei festgelegten Punkten aus mit dem Radius R verbunden werden.
Lösung: Von den festgelegten Punkten aus Kreisbögen mit R schlagen. In ihrem Schnittpunkt liegt der Einstichpunkt für den Zirkel.
Aufgabe e) Zwei Kreisbögen mit den Radien R1 und R2 sollen miteinander verbunden werden; dabei soll M2 um das Maß a oberhalb von M1 liegen.
Lösung: Die Mitte M2 liegt auf einem Bogen, der von M1 aus den Abstand (R1 + R2) besitzt. Diesen Bogen bringt man mit der waagrechten Linie Abstand a zum Schnitt und erhält M2. Der Anschlusspunkt zwischen beiden Kreisbögen liegt auf der Verbindungslinie zwischen M1 und M2.