Geometrie und Rechnen 02.07.2016, 05:17
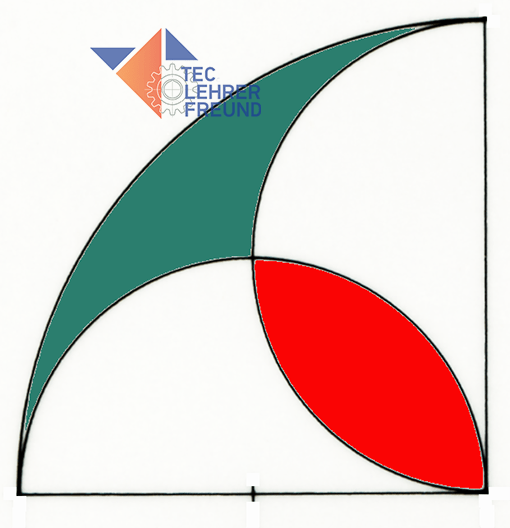
In einen einfachen Viertelkreis sind zwei Halbkreise eingeschrieben. Zeichnet man sie mit dem Zirkel, entstehen zwei Restflächen, die angeblich gleich groß sind. Vergleichen nach Gefühl reicht nicht aus; also müssen wir ein bisschen rechnen.
Japanische Ornamentik

Der Japaner Kobon Fujimura hat einen nicht alltäglichen Beruf gewählt: Er erfindet Rätsel. In seinem Buch »The Tokyo Puzzle« verblüfft er den Leser mit geometrischen Spielereien, wie die folgende Aufgabe zeigt.
In einen Viertelkreis mit dem Radius r sind zwei Halbkreise eingezeichnet, deren Durchmesser dem Radius des Viertelkreises entsprechen. Durch die Konstruktion entstehen zwei geschlossene Flächen, die wir in unserer Skizze rot und grün gekennzeichnet haben.
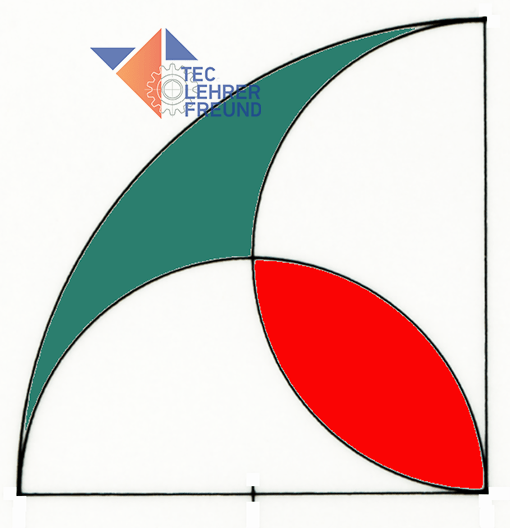
Fujimura behauptet, die grüne Fläche A1 und die rote Fläche A3 seien gleich groß. Das sollen wir nachweisen.
Ein Tipp: Ob Fujimura Recht hat, bekommen wir nur mit einer kleinen Rechnung heraus. Sie beruht auf der Formel für die Berechnung einer Kreisfläche: Ages = r2 • π
Lösungswege
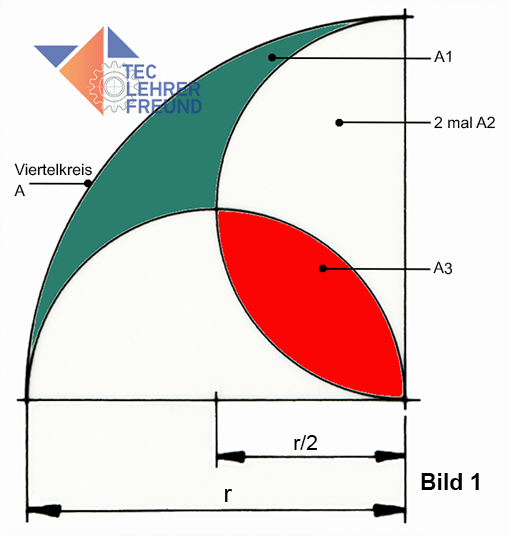
a) Skizze mit Viertelkreis (Bild 1)
Die Teilflächen heißen A, A1, 2 mal A2 und A3. Die beiden Halbkreise überlappen sich; so entsteht die blattförmige Teilfläche A3.
Viertelkreisfläche A = r2 · π : 4
1 Halbkreisfläche A2 = 1/2 · (r/2)2 · π = r2 · π : 8
2 Halbkreisflächen 2 · A2 = 2 · r2 · π : 8 = r2 · π : 4
Die Viertelkreisfläche A setzt sich zusammen aus A1 + 2 · A2; A3 muss abgezogen werden, sonst zählt sie doppelt.
A = A1 + 2 · A2 – A3 ––>
r2 · π : 4 = A1 + r2 · π : 4 – A3
0 = A1 – A3
A1 = A3
b) Eine zweite Möglichkeit: Wir ergänzen die Viertelkreisfigur in Bild 1 zu einem ganzen Kreis (Bild 2).
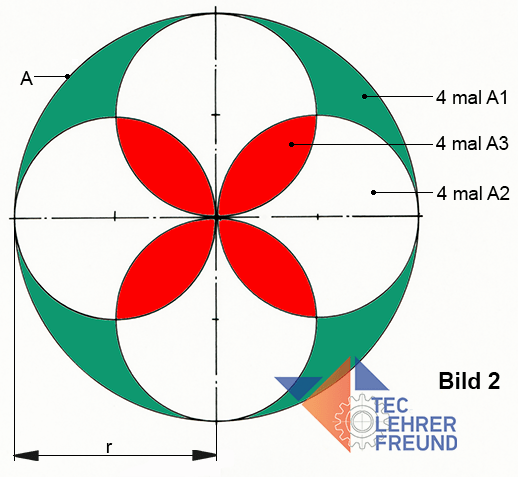
Der große Kreis hat den Radius r. Der Durchmesser der vier kleinen Kreise ist dann ebenfalls r.
Die Fläche des großen Kreises ist r2 · π. Sie ist die Summe der Flächen
• der vier grünen Teilflächen,
• der vier weißen Kreisflächen,
• minus den vier roten, blattförmigen Teilflächen.
Auch hier müssen wir die roten Flächen abziehen, weil sie sonst doppelt gezählt würden.
A = r2 · π
4 · A2 = 4 · (r/2)2 · π = r2 · π
A setzt sich zusammen aus 4 · A1 + 4 · A2 – 4 · A3 ––>
A = 4 · A1 + r2 · π – 4 · A3 ––>
r2 · π = 4 · A1 + r2 · π – 4 · A3
0 = A1 – A3
A3 = A1
In beiden Fällen a) und b) ergibt sich: A3 = A1, d.h. die beiden Flächen A3 und A1 sind – da hat Fujimura also recht – gleich groß.