Festigkeitsberechnungen (6): Abscherung 09.05.2012, 07:02
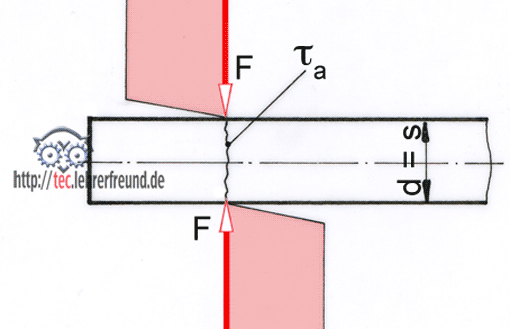
Bei einer Beanspruchung auf Abscherung entstehen in einer Querschnittsfläche Spannungen, die parallel zur angreifenden Kraft liegen.
Abscherbeanspruchung (Abscheren)
Die äußeren Kräfte wirken senkrecht zur Stabachse. Sie versuchen die beiden Schnittufer parallel zueinander zu verschieben. Die innere Kraft F liegt parallel zur Schnittfläche, dabei entstehen Schubspannungen τ (griech. Buchstabe tau = Abscherspannungen). Auf Abscherung beanspruchte Bauteile dürfen nicht zerstört werden. Ausnahme: Beim Schneiden von Blechen findet eine Werkstofftrennung statt. Bei der Auswahl der Spannungsgrenzwerte ist zu prüfen, ob es sich um eine Abscherung oder ein Schneiden handelt.
Bezeichnungen:
F Scher-, Schneidkraft N
S Querschnittsfläche mm2
τa Scherspannung N/mm2 (τ = tau, griech. Buchstabe)
τaB Scherfestigkeit N/mm2
τaB max maximale Scherfestigkeit N/mm2
Rm max maximale Zugfestigkeit N/mm2
ν Sicherheitszahl (ν = nü, griech. Buchstabe), ohne Einheit
Die Querschnittsfläche S besteht aus der Summe der Scherflächen, die beim Durchtrennen Bruchflächen ergeben.

Beanspruchung auf Abscherung
Durchgeführt werden die Festigkeitsberechnungen mit den durch Versuche ermittelten oder Tabellen entnommenen Scherfestigkeiten τaB. Für Stahl gilt näherungsweise auch τ0,8 • Rm
Formeln zusammengefasst:
Scherspannung τa = F : S
Zulässige Scherspannung τa zul = τaB : ν
Scheidkraft F = S • τaBmax
Maximale Scherfestigkeit τaBmax = 0,8 • Rm max
Berechnungsbeispiel
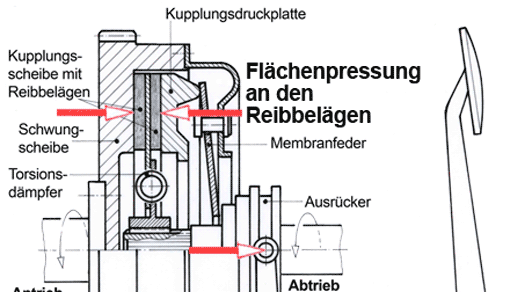
Bild oben: Mit welcher Scherkraft F wird der Bolzen aus S275J2G3 in der zweischnittigen Verbindung belastet? Gegeben: Bolzenquerschnitt S = 201 mm2; Scherfestigkeit τaB = 440 N/mm2; Sicherheitszahl ν = 1,6.
Lösung:
F = 2 • S • τazul
τazul = τaB : ν = 440 = N/mm2 : 1,6 = 275 N/mm2
F = 110 550 N = 110,55 kN
Schneiden von Werkstoffen (Bild unten)
Zur Berechnung der Schneidkraft F ist die maximale Scherfestigkeit τgB max einzusetzen. Ist diese nicht bekannt, kann man näherungsweise auch mit der Zugfestigkeit rechnen: τgB max = 0,8 • Rm max.
Beispiel: Eine Scheibe mit einem Durchmesser d = 24 mm wird aus Stahlblech S275J2 mit einer Dicke s = 4 mm ausgeschnitten (Bild). Die Zugfestigkeit Rm max dieses Stahles liegt zwischen 410 N/mm2 und 560 N/mm2. Welche Scherkraft F muss aufgebracht werden?
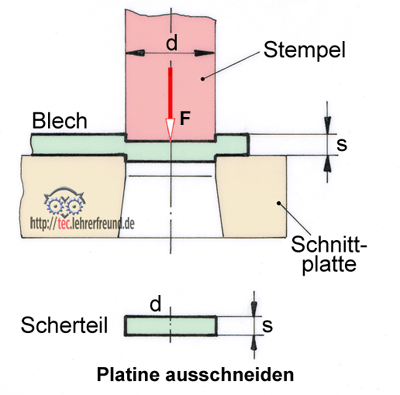
Lösung:
Scherkraft F = S • τaBmax
Scherfläche S = Umfang U • Dicke s = π • d • s =
S = π • 24 mm • 4 mm = 301,6 mm2
F = 301,6 mm2 • 0,8 • 560 N/mm2 =
F = 135 117 N = 135,1 kN