Fahrrad-Nabenschaltungen (1) 29.11.2012, 06:16
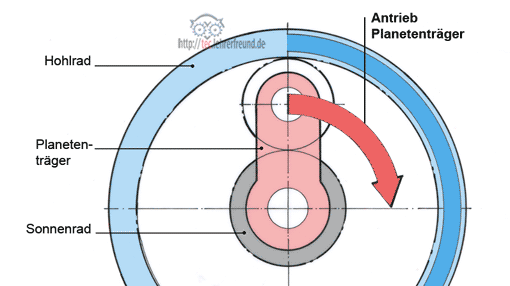
Die Basis aller Fahrrad-Nabenschaltungen sind Planetengetriebe in verschiedenen Ausführungen. Das einfachste Planetengetriebe erlaubt das Fahren mit drei Gängen. Hier einführende Grundlagen dazu.
Fahrrad-Nabenschaltung
Die Tretkraft des Radfahrers ist begrenzt; wenn sie auf ebener Strecke zum Fahren ohne Gangschaltung ausreicht, genügt sie an längeren Steigungen nicht mehr. Die Fahrradschaltung hat die Aufgabe, die Antriebskraft an unterschiedliche Fahrwiderstände anzupassen. Fahrräder können mit zwei Schaltsystemen ausgestattet sein: mit Nabenschaltungen und Kettenschaltungen.
Nabenschaltungen
Weil sie geschlossen in der Hinterradnabe von Zweirädern eingebaut sind, sind die Getriebe-Einzelteile gegen Verschmutzung geschützt. Im Gegensatz dazu sind Kettenschaltungen offen und damit äußerer Verschmutzung ausgesetzt.
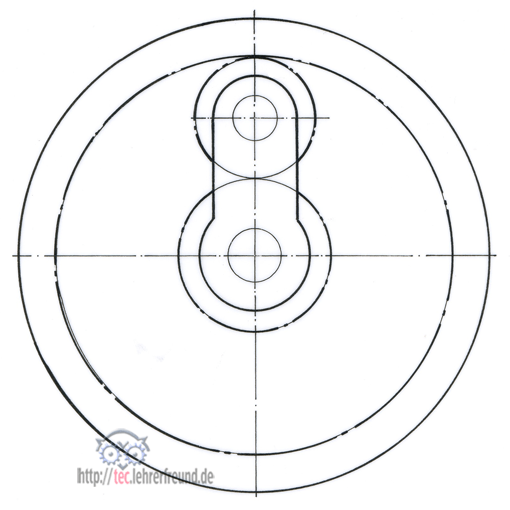
Die Basis aller Nabenschaltungen sind Planetengetriebe in verschiedenen Ausführungen. Das einfachste Planetengetriebe erlaubt das Fahren mit drei Gängen. Die folgenden Erläuterungen und ein weiterer Beitrag befassen sich mit einem solchen 3-Gang-Planetengetriebe. Dazu sei auch auf die tec.LEHRERFREUND-Beiträge Planetengetriebe (1) und Planetengetriebe (2) verwiesen.
Oft wird auch die Kettenschaltung mit einer Nabenschaltung kombiniert. Die Kombination 3-Gang-Nabenschaltung mit 7-Gang-Kettenschaltung ergibt dann eine Schaltung mit 7 mal 3 = 21 Gängen.
Schalten: Die Nabenschaltung wird mit einem Schalter am rechten Lenkergriff betätigt. Dabei ist kein Treten wie bei Kettenschaltungen notwendig. Beim Schalten während der Fahrt ist es schonend für die Getriebebauteile, wenn man mit etwas weniger Kraft weiter tritt. Schädlich ist das Schalten unter Volllast.
Kenngrößen einer Gangschaltung sind neben der Anzahl der Gänge der Übersetzungsbereich, also das Verhältnis zwischen größtem und kleinstem Gang. 3-Gang-Nabenschaltungen besitzen Übersetzungsbereiche von etwa 180 %; bei 7-Gang-Naben geht sie bis 300 %. Der Hersteller ROHLOFF gibt für seine 14-Gang-Nabe SPEEDHUB einen Übersetzungsbereich von weit über 500 % an. (Diese Schaltung ist die einzige unter Last schaltbare Nabe).
Beachten: Übersetzungen in der Fahrradtechnik
Übersetzungen bei Fahrrädern wurden schon immer anders berechnet als Übersetzungen im allgemeinen Maschinenbau.
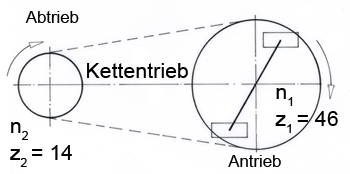
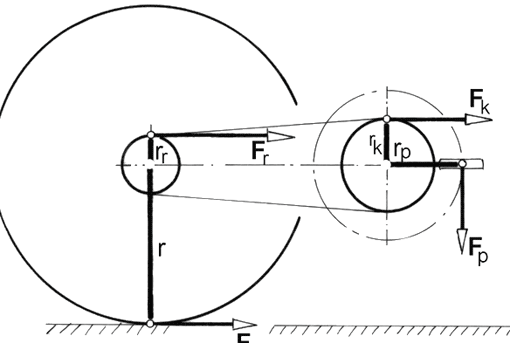
In der Fahrradtechnik ist die Übersetzung (Skizze)
i = z1 : z2 (im Maschinenbau ist es umgekehrt: i = z2: z1)
i = n2 : n1
In Zahlen: i = z1 : z2 = 46 : 14 = 3,286, d.h. die Übersetzung ins Schnelle ergibt eine Zahl >1.
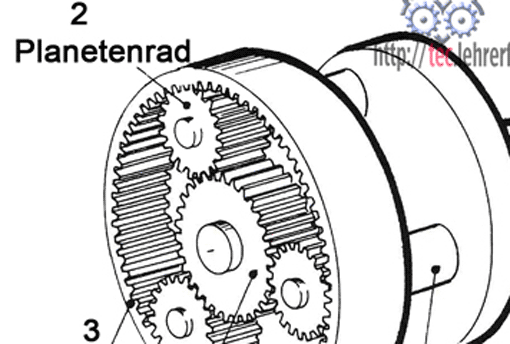
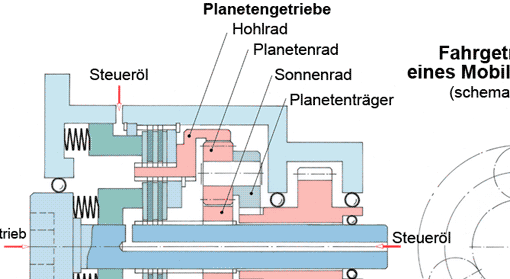
Fahrrad: Sonnenrad steht, Planetenträger treibt Hohlrad an.
Um das auf der Hinterachse feststehende Sonnenrad drehen sich drei Planetenräder (im Bild ist nur ein Rad gezeichnet). Dabei treibt der Planetenträger über das Planetenrad das Hohlrad und die Nabe an. In den Skizzen ist der Planetenträger als Hebel dargestellt. In der konkreten Konstruktion jedoch ist es in der Regel ein geteilter Scheibenring, in dem die drei Planetenräder gelagert sind.
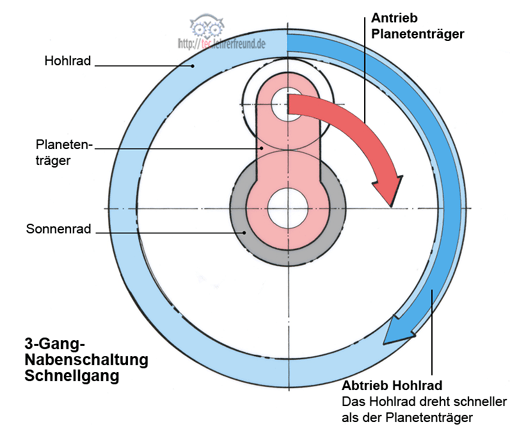
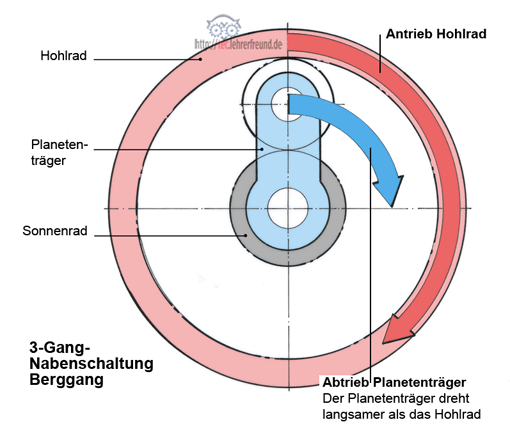
3-Gang-Planetengetriebe: Berechnungsbeispiel Schnellgang
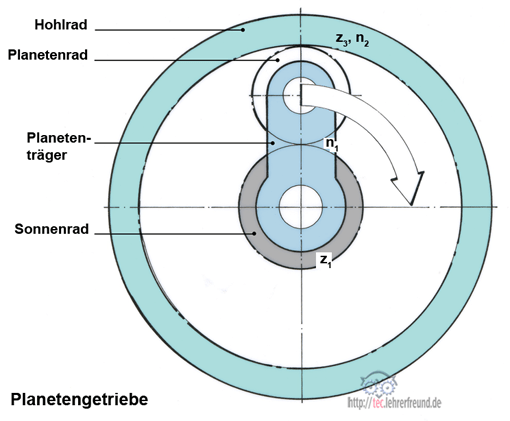
Wie oft dreht sich bei 1 Umdrehung des Planetenträgers das Hohlrad?
Man kann sich den Vorgang so vorstellen:
In Gedanken blockiert man Sonnenrad 1 und Planetenrad 2 miteinander.
Schritt 1: Man dreht den Planetenträger 1 Umdrehung nach rechts, dabei machen auch das Sonnenrad und das Hohlrad 1 Umdrehung nach rechts.
Schritt 2: Weil das Sonnenrad hätte stehen bleiben müssen, heben wir die Blockierung auf und drehen das Sonnenrad bei festgehaltenem Planetenträger wieder 1 Umdrehung zurück. Dabei dreht sich das Hohlrad im Verhältnis der Zähnezahlen z1 : z3 weiter nach rechts.
Bei 1 Umdrehung des Planetenträgers dreht sich das Hohlrad also 1 + z1: z3 Mal.
Rechenbeispiel dazu:
z1 = 13, z3 = 45, n1 = 150 1/min.
i = 1 : (1 + 13 : 45) = 1 : 1,289 = 0,776, das ist eine Übersetzung ins Schnelle.
n2 = n1 : i = 150 : 0,776 = 193,3 1/min.
Aufgabe: Bestimmen Sie die Abtriebsdrehzahl n des Hohlrades und das Übersetzungsverhältnis i einer 3- Gang-Nabenschaltung.
Gegeben sind: Zähnezahl z1 des Sonnenrades = 17, Zähnezahl des Hohlrades z3 = 51, Antriebsdrehzahl des Planetenträgers n1 = 160 U/min.
Lösungen:
i = 0,75
n2 = 213,33 1/min
Die Skizze unten ist für die Verwendung in Aufgabenblättern gedacht.