Die Kugel und ihre Abwicklung 18.07.2012, 07:06
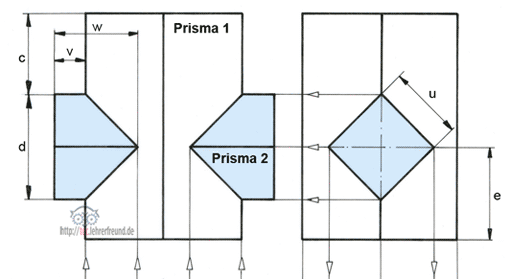
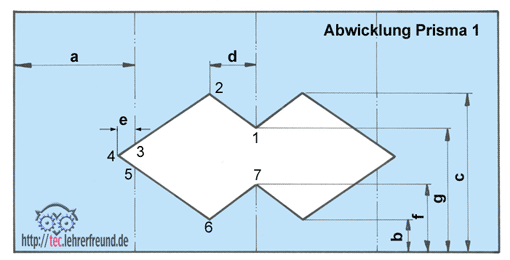
Beim Zeichnen der Oberfläche eines (dreidimensionalen) Körpers in der Ebene auf ein Papierblatt erhält man eine so genannte Abwicklung der Körperoberfläche. Wir haben ihre Konstruktion schon bei prismatischen Körpern besprochen. Wie sieht sie bei einer Kugel aus?
Wenn man die Oberfläche eines (dreidimensionalen) Körpers in der Ebene (z. B. ein Papierblatt) zeichnet, erhält man eine Abwicklung der Körperoberfläche.
Idee: Sie möchten einen Globus basteln. Dafür hätten Sie als Grundkörper eine Holzkugel mit 20 cm Durchmesser zur Verfügung. Auf diese Kugel wollen Sie einen Papierbogen mit dem aufgemalten Erd-, Mond- oder sonst einem Motiv kleben.
Frage: Wie muss der auf die Kugel passende Papierbogen ausgeschnitten werden?
Wir gehen gute 500 Jahre zurück. Damals lebte in Süddeutschland ein berühmt gewordener Kartograf - ein Mensch, der Weltkarten malte. Es war Martin Waldseemüller (ca. 1470 - 1520). Von ihm stammt die erste Weltkarte, auf der die westlichen Landmassen der Erde den Namen »America« erhielten - benannt nach dem Italiener Amerigo Vespucci. Waldseemüller war der Meinung, der Seefahrer Vespucci - und nicht Kolumbus - habe den neuen Kontinent entdeckt. Von Waldseemüller fand man im Juni 2012 in München den Druck einer Weltkarte, die unsere obige Frage beantwortet.
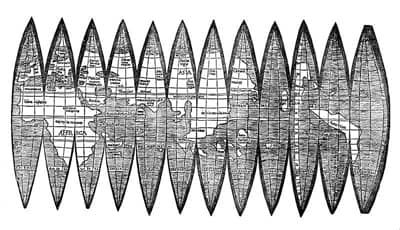
Bild: Martin Waldseemüller: Die Erdglobus-Segmentkarte von 1507 (Public Domain)

Bild: Deutsche Briefmarke 2,20 Euro
Wie Waldseemüller auf die flachspitzige Form kam, wissen wir nicht; vielleicht hat er sie von einer geschälten Orange abgespickt. Ganz sicher hat er immer wieder Versuche mit Kugeloberflächen angestellt und erkannte als geschulter Geometer sehr schnell, dass die abgewickelte Form so aussehen musste.
Bild unten: Massimo L.: Citrus sinensis (L.) Histoire et culture des orangers A. Risso et A. Poiteau. - Paris Henri Plon, Editeur, 1872. (Public Domain)

Die Kugel hat Eigenschaften, die es uns mehr als schwer machen, ihre Oberfläche auf ein glattes Stück Papier zu bringen: Sie besitzt weder Kanten noch Ecken, und Menschen, die sie genau studiert haben, behaupten: Ihre Oberfläche lässt sich nicht in der Ebene ausbreiten.
Andere Eigenschaften der Kugel:
- Von allen Körpern mit einem vorgegebenen Volumen hat die Kugel die kleinste Oberfläche.
- Von allen Körpern mit vorgegebenem Flächeninhalt umschließt sie das größte Volumen.
- Die Kugel besitzt unendlich viele Symmetrieebenen; sie gehen alle durch den Kugelmittelpunkt.
- Eine Kugel kann als Rotationskörper aufgefasst werden: Lässt man eine Halbkreisfläche um ihre Achse rotieren, dann ist der dabei entstehende Rotationskörper eine Kugel.
Eine Kugel abwickeln
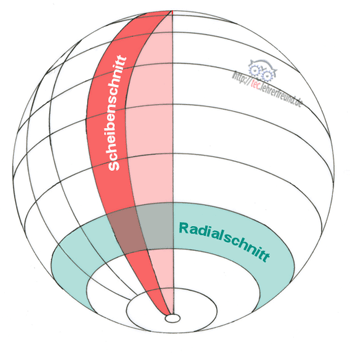
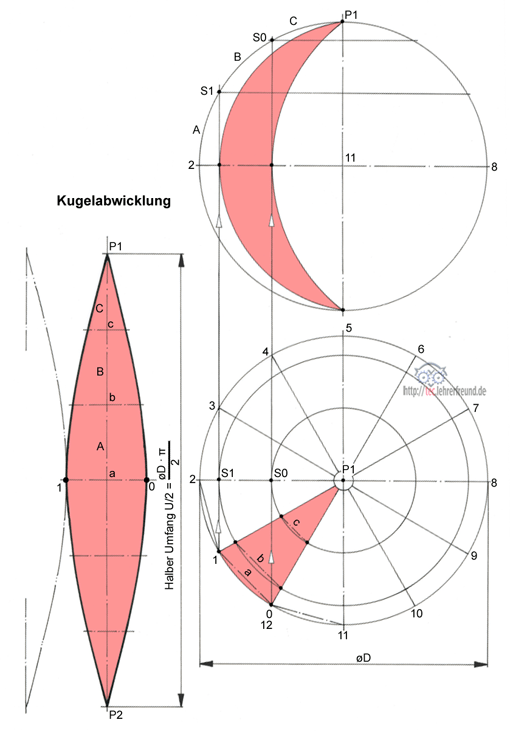
Eine Kugelabwicklung lässt sich auf zwei Arten konstruieren: mit Radialschnitten oder mit parallelen Scheibenschnitten. Wir schließen uns hier Martin Waldseemüller an und wählen die Scheibenschnitt-Methode. Dabei teilt man den Kreis in beliebig viele, gleiche Teile, z. B. 12 oder 16, ein. Die entsprechenden Teilungspunkte verbindet man durch Geraden (z. B. 0 - 6; 1 - 7 usw.), die durch den Kugelmittelpunkt gehen.
In der Skizze oben ist eine Kugel in Vorderansicht und Draufsicht dargestellt.
Draufsicht: Sie ist gleichmäßig geteilt, hier zwölf Mal, mit Nummerierung am Außenkreis von 0 bis 12. Von den Punkten 0 und 1 fällt man Lote auf die Mittellinie 2 – 8 und zieht diese durch in die Vorderansicht. In der Draufsicht ergeben die Lote die Schnittpunkte S0 und S1, ebenso in der VA.
Vorderansicht: Zieht man von S1 und S0 aus waagrechte Linien, dann schneiden diese aus der Kugel waagrechte Scheiben heraus, die wir in die Draufsicht als Kreise einzeichnen; sie gehen dort ebenfalls durch S1 und S0. In der Vorderansicht sind die Bogenstücke 2 – S1, S1 – S0 und S0 – P1 gleich lang. Diese Behauptung wollen wir den Obermathematikern glauben; sie erlassen es uns, die Konstruktion beweisen zu müssen.
Damit können wir die rot angelegte Zwölftel-Kugelabwicklung zeichnen. Auf der Mittellinie P1 – P2 tragen wir 6 gleich lange Teile ab. Dann übertragen wir aus der Kugel-Draufsicht die Abstände a, b und c in die Abwicklung.
Mit dem Kurvenlinieal verbinden wir die gefundenen Punkte zum abgewickelten Segment.
Anmerkung: Werden die Einzelabwicklungen zu einer Kugel zusammengebogen, dann wäre eine saubere Kugelform, auch in Umfangsrichtung, kaum ohne Gewaltanwendung denkbar. Wir werden also nur eine angenäherte Kugel erhalten mit in Umfangsrichtung zwölf ebenen Einzelsegmenten. Solche kann man zum Beispiel bei vielen Zwiebeltürmen beobachten.

Bild WIKIPEDIA
________________________
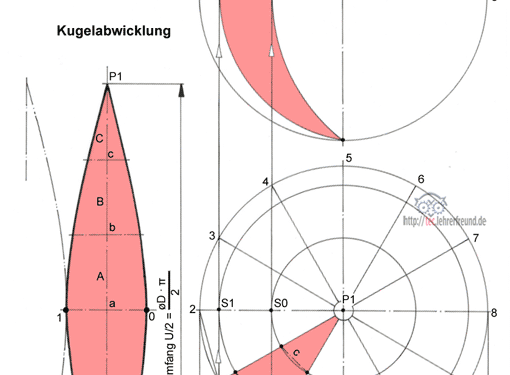
Die unvollständige Skizze unten ist für die Verwendung in Aufgabenblättern gedacht.