Deutsch im technischen Unterricht: Technisches Experiment (4) 11.09.2015, 05:35

Ein Steinmetz muss ein altes Sandsteinfenster sanieren. Bei der Anfertigung der Zeichnung ist ihm zunächst nicht klar, wie ein Leibungsprofil aussieht, wenn es auf eine schräge Simsfläche trifft. Er fertigt ein einfaches Modell an und findet damit die Lösung. Diese soll er vor seiner Klasse erläutern.

4. Wortschatz im technischen Unterricht: Technisches Experiment 

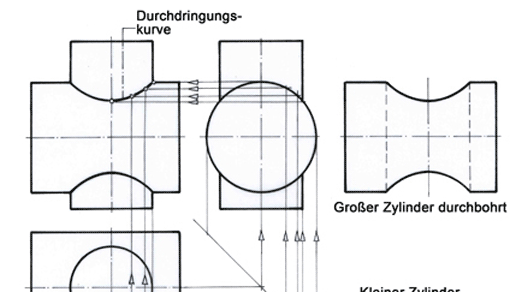
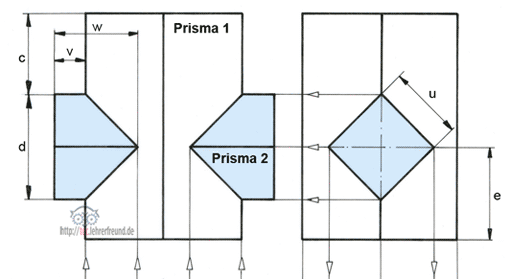
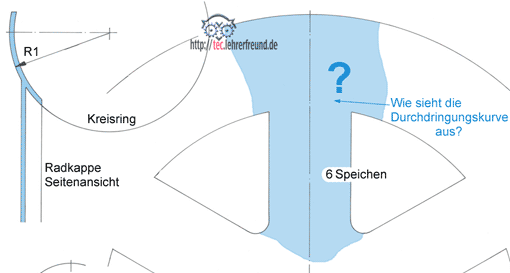
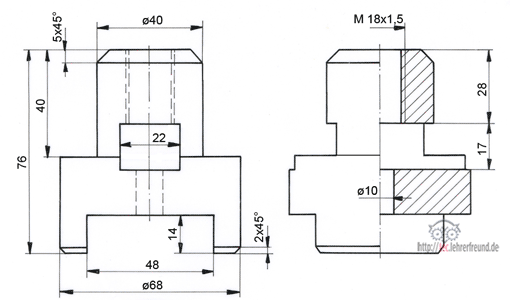
Problemstellung: Ein Steinmetz soll ein Kapellenfensters zeichnen. Dieses besteht aus einem abgeschrägten Sims und der aus Profilteilen hergestellten Leibung; alle Teile sind aus rotem Sandstein gefertigt (Zeichnung Bild 1). Der Steinmetz hat ein Problem mit dem in Bild 1 eingekreisten Detail, also dort, wo die Kehle des Profilstabs auf die schräge Simsfläche trifft. Die Hohlkehle stellt in der Draufsicht einen Viertelkreis dar (Zeichnung Bild 2). 

Bild 1: Profilteil trifft auf ein schräg verlaufendes Sims (Kreis)

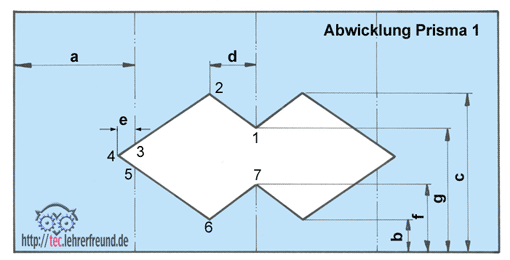
Bild 2: Quer durchgeschnittenes Profilteil

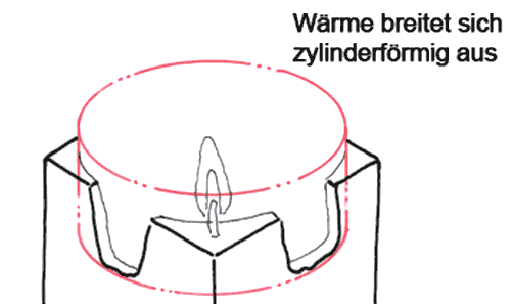
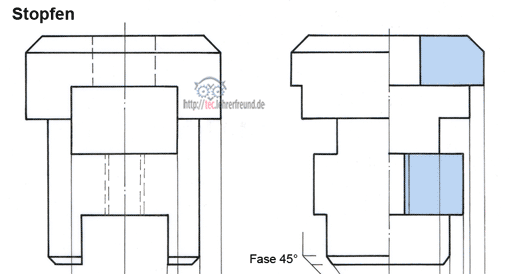
Um sein Problem zu lösen, behilft sich der Steinmetz mit einem einfachen Modell, das er selbst anfertigt (Bild 3). 

Bild 3: Modell

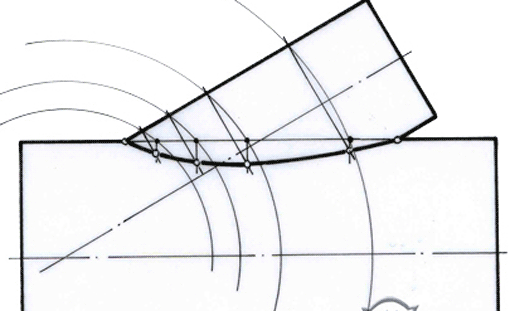
Dieses Modell soll er seiner Klasse erläutern, in der es Schüler gibt, denen die Verschneidung zwischen Profilstab und Simsfläche anfangs auch nicht klar ist. Darüber hinaus soll er seinen Mitschülern eine Anleitung geben, wie man die drei vorgegebenen Ansichten in Zeichnung Bild 4 fertigstellt. Bild 5 zeigt die Lösung. 

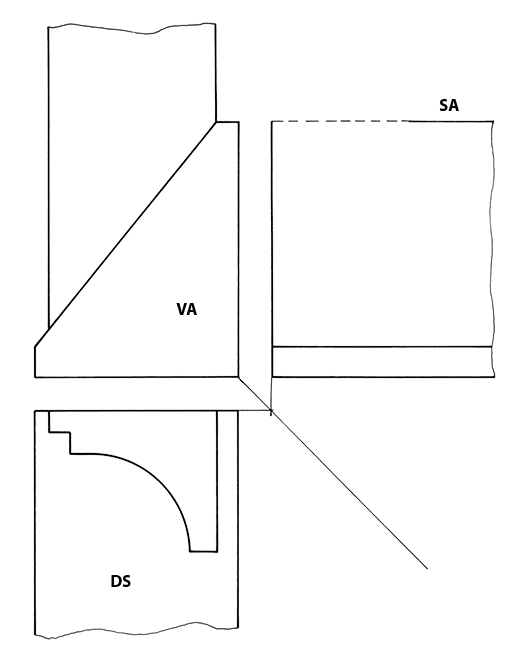
Bild 4: Wie sieht das Profilteil in Vorderansicht und Seitenansicht aus?

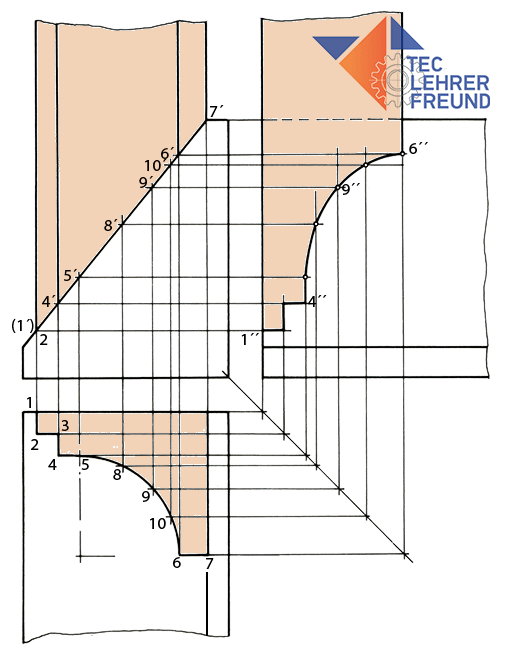
Bild 5: Lösung

Eine zusätzliche Aufgabe soll den Zuhörern die Möglichkeit geben, das Gelernte zu vertiefen.

Anmerkung: Der Vortragende muss davon ausgehen können, dass die Zuhörer die Regeln und die Entstehung der Dreitafel-Projektion beherrschen. 

1. Vorstellung der Aufgabe

Anmerkung: Für seinen Vortrag stehen dem Vortragenden alle hier verwendeten Bilder zur Verfügung.

Hinleitung: Kapelle aus dem 19. Jahrhundert mit Sandsteinfenstern, die saniert werden müssen (Bild 1). 

»Als ausführender Steinmetz musste ich zunächst von einem der Fenster eine Skizze aufnehmen und diese bemaßen. Danach war eine maßstabsgetreue Zeichnung anzufertigen. Dabei stand ich vor der Frage: Wie sieht die Durchdringungslinie aus, wenn das senkrecht eingebaute Profilstück (Bild 2) mit seiner Stirnseite auf ein schräges Gesims trifft?  
(Falls der Begriff »Durchdringungslinie« den Zuhörern Schwierigkeiten bereitet, muss ich ihn an dieser Stelle klären. Ich würde dafür die Erläuterungen im tec.LEHRERFREUND-Beitrag Durchdringungen (3) heranziehen).

In meiner Zeichnung (Bild 4) gelang es mir anfangs nicht, die Lösung in der Seitenansicht zu finden.  

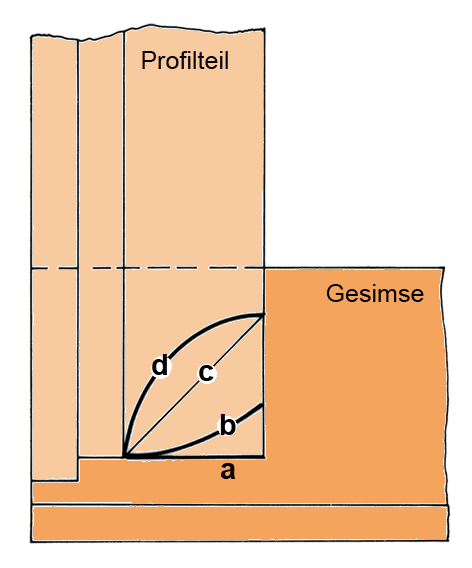
Bevor ich nun weiterfahre, hätte ich gerne, dass eine/r von Euch versucht, den ihrer/seiner Meinung nach richtigen Kurvenverlauf in der Seitenansicht auszuwählen. Bild 6 unten: Eine der vier Verschneidungslinien a), b), c), d) ist richtig, welche?«
(Damit erreicht der Vortragende, dass seine Zuhörer ein Gefühl für den Schwierigkeitsgrad der Aufgabe bekommen). 

2. Erläuterung des Modells 

»Ich selbst behalf mir mit einem einfachen Modell (Bild 3), das ich Euch vorstellen möchte.
Sein Herzstück ist der von einer Haushaltsrolle stammende Pappzylinder. Die Simsfläche war ein stabiler Pappdeckel, den ich schräg stellte. Die Schräge habe ich auf ca. 60° vergrößert, damit der Bogenverlauf deutlicher wird.

Die Hohlkehle ist Teil eines Zylinders. Der Pappzylinder half mir, die Hohlkehle auf den Pappdeckel, also auf die schräge Gesimsfläche aufzusetzen. Weil sie zunächst nicht passte, schnitt ich ihr Ende mit der Schere so zurecht, dass die entstandene Schräge satt auf der Gesimsschräge aufsaß. (Ebenso hätte ich eine schräg abgeschnittene Plastik-Wasserflasche verwenden können). 
Mit einem Filzstift ummalte ich die Sitzfläche (-linie). Nun war mir klar, welche Form die Verschneidung des Viertelkreises mit der Gesimsfläche hat: Sie ergibt eine wie in d (Bild 6) gezeigte Viertel-Ellipse.  
Das größte Problem dabei war, dass ich nicht sofort erkannte, dass in der geschlossenen 360°-Pappröhre die 90°-Hohlkehle versteckt ist. Diese Ellipse musste ich nun maßstabsgetreu in meine unvollständige Seitenansicht bringen.

3. Erklärung der Dreitafel-Projektion

Ich erkläre Euch im Folgenden, wie man den Ellipsenverlauf zeichnerisch in der Seitenansicht ermittelt.  
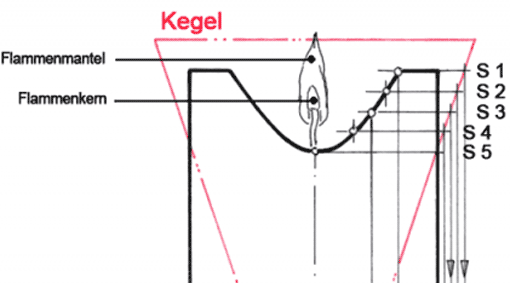
Bild 5: In der Draufsicht DS erscheint der Querschnitt des Profilstücks unverzerrt. Die Abmessungen des Querschnitts habe ich bei meiner vorausgehenden Modellaufnahme ermittelt.   
Man kennzeichnet in der DS die Ecken des Profils und nummeriert sie; hier sind es die Zahlen von 1 bis 7. Auch auf dem Viertelkreisbogen der Hohlkehle markiert man gleichmäßig verteilt drei Punkte; ich habe sie mit 8, 9 und 10 nummeriert.

Die Punkte 1 bis 10 projiziert man nach oben in die Vorderansicht und über die 45°-Spiegelgerade in die Seitenansicht. Zusammen mit den Projektionslinien aus der Vorderansicht VA ergeben sich in der Seitenansicht SA die Punkte, die auf der Durchdringungslinie liegen. Verbindet man diese miteinander, dann entsteht die gesuchte Durchdringungslinie.«

(Ob den Zuhörern damit alles einleuchtet, ist fraglich. Lässt man sie aber an einer vereinfachten Aufgabe das Vorgetragene Schritt für Schritt in Eigenarbeit wiederholen, werden sie das Problem verinnerlichen.) Dafür wäre die folgende Aufgabe tauglich.

Übungsaufgabe: 

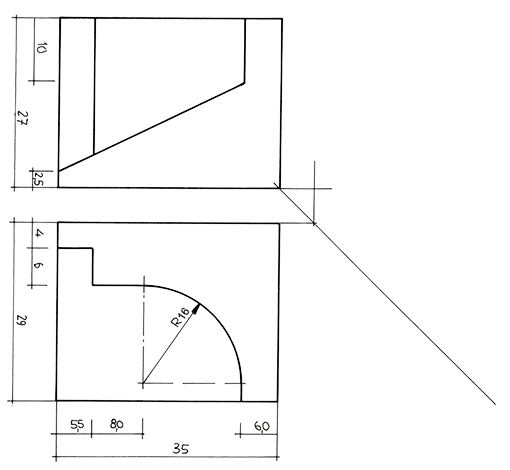
Bild 7a: Übungsaufgabe, bemaßt 

Die Übungsaufgabe beinhaltet das in der Präsentation verwendete Profil-Sandsteinteil, ist aber mit dem Sims zu einem einzigen Teil zusammengefasst.

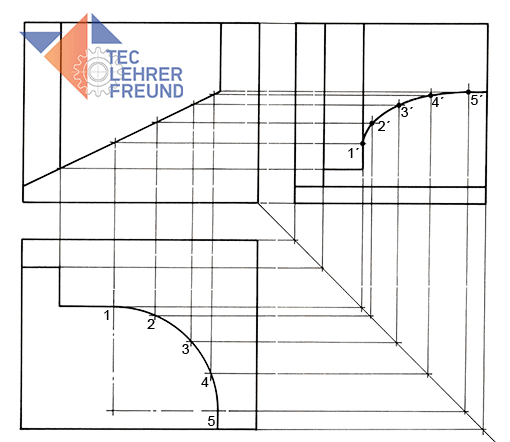
Bild 7b: Übungsaufgabe, Lösung

Letzte Zweifel werden mit der perspektivischen Darstellung des Profilstücks (Bild 8) ausgeräumt. Für den Schüler wäre es eine reizvolle Aufgabe, die Perspektive selbst zu zeichnen.

Bild 8: Übungsaufgabe perspektivisch

Anmerkungen zur sprachlichen Darstellung  

Bis zu »3. Erklärung der Dreitafel-Projektion« musste der Schüler Vorarbeiten beschreiben, die vor dem Präsentationstermin lagen. Es war konsequent, dies in der Vergangenheit zu tun. 

Im Vortrag verwendete Fachbegriffe:  

Draufsicht 
Durchdringungslinie  
Hohlkehle  
Modell 
Modellaufnahme  
Profilstück 
Projektionslinien  
Seitenansicht  
Simsfläche  
Verschneidung 
Viertelkreisbogen  
Vorderansicht