Bohrmaschinen-Ständer (2): Lösung der Kräfte-Aufgaben 19.01.2012, 15:31

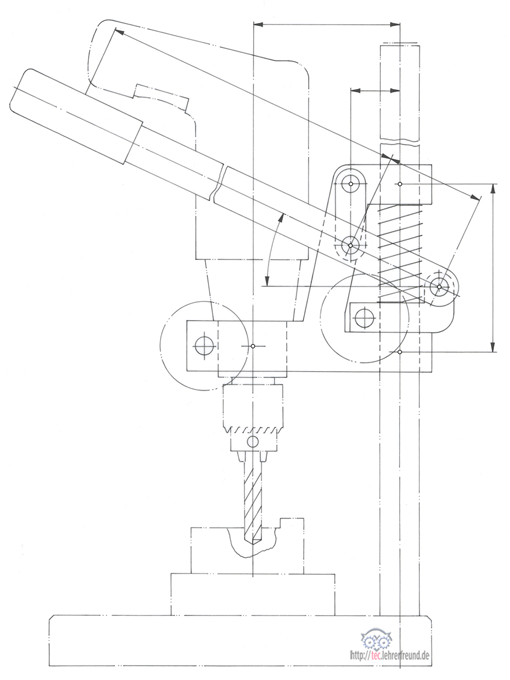
Bohrmaschinen-Ständer: Die auf den Vorschubhebel und die Führungsgabel wirkenden Kräfte werden mit Hilfe der Gleichgewichtsbedingungen ermittelt. Mit Skizzen für Arbeitsblätter.

Aufgabe 1.

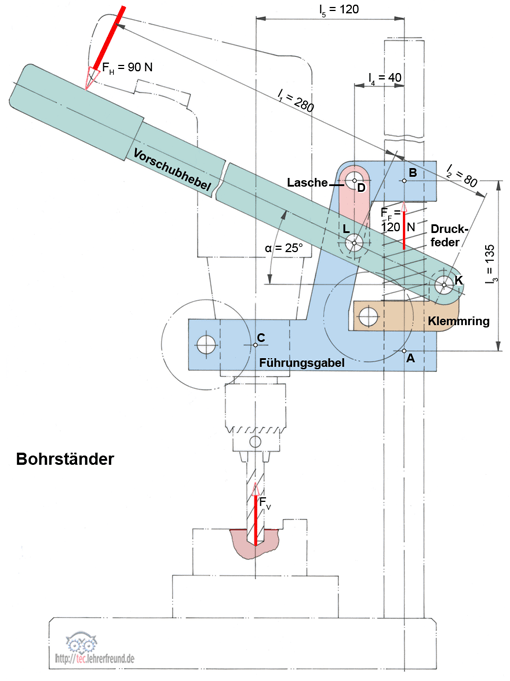
Vorschubhebel:

F_L und F_K berechnen.

Wir wiederholen die Lösungsschritte:
- Sich über die Funktion der Baugruppe klar werden
- Den als  Aufgabe gestellten Körper freimachen
- Das geeignete Kräfteverfahren wählen
- Die Aufgabe lösen

Funktion
Mit dem Klemmring wird die Bohrmaschinenhöhe eingestellt. Auf dem Klemmring stützt sich die Druckfeder ab und drückt die Führungsgabel nach oben, bis sie von unten her am Klemmring anschlägt.
Der Klemmring ist gleichzeitig Lager für den Vorschubhebel. Wird gebohrt, d. h. der Vorschubhebel nach unten bewegt, drückt er über die Lasche die Führungsgabel und damit die Bohrmaschine nach unten.

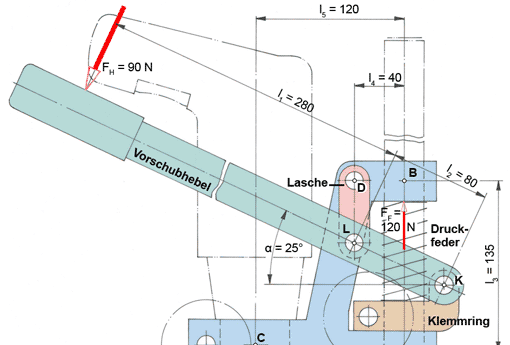
Vorschubhebel freimachen 

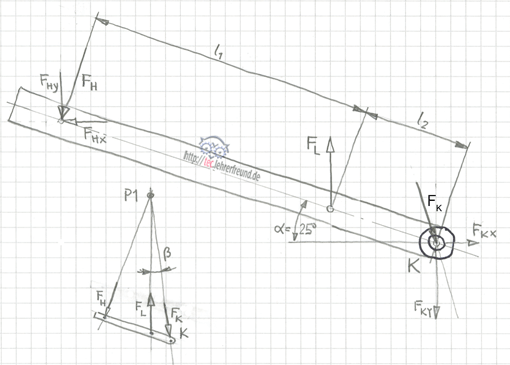
Der unter 25° geneigte Vorschubhebel wird beim Bohren mit der Handkraft F_H nach unten gedrückt; F_H ist nach Betrag und Richtung bekannt. Die Laschenkraft F_L ist nach ihrer Richtung bekannt: Die Lasche ist ein Zweigelenkstab, der nur in seiner Achse Kräfte übertragen kann. K ist ein zweiwertiges Lager, über das man sonst nichts weiß. Deshalb tragen wir die x- und die y-Komponente ein.

Kleine Skizze: Über die Richtung von F_K können wir uns Klarheit verschaffen, wenn wir den Regeln zum 3-Kräftesystem folgen: Bringen wir die Kräfte F_H und F_L, deren Wirklinien ja bekannt sind, zum Schnitt in P1, dann muss auch die Lagerkraft F_K durch den Punkt P1 gehen (Erläuterungen dazu im Beitrag »Kräfte: Unbekannte Kräfte zeichnerisch ermitteln (1)«).

Berechnungen

Gleichgewichtsbedingungen
ΣF_x = 0 = - F_Hx + F_Kx  –> F_Kx = F_Hx
Nebenrechnung: sin α = F_Hx : F_H  –> F_Hx = F_H ∙ sin α = 90 N ∙ 0,423 = 38,0 N
F_Kx = F_Hx = 38,0 N
cos α = F_Hy : F_H –> F_Hy = F_H ∙ cos 25° = 81,6 N

ΣF_y = 0 = - F_Hy + F_L - F_Ky  –>  F_L über Gleichgewichtsbedingung ΣM_(K) = 0 berechnen

ΣM_(K) = 0 = F_Ly ∙ l₂ - F_H ∙ (l₁ + l₂)
F_L ∙ cos α ∙ l₂ - F_H ∙ (l₁ + l₂)
F_L = F_H ∙ (l₁ + l₂) : (cos α ∙ l₂) = 90 N ∙ 360 mm : (0,906 ∙ 80 mm)
F_L = 447 N

ΣF_y = 0 = - F_Hy + F_L - F_Ky –>
F_Ky = F_L - F_Hy = 447 N - 81,6 N = 365,4 N
F_K = √F_Kx² + F_Ky²    = √38,0² N² + 365,4² N²   =
F_K = 367,4 N

sin β = F_Kx : F_K = 38,0 N : 367,4 N = 0,103  –>  β = 6° 12´

Aufgabe 2. 

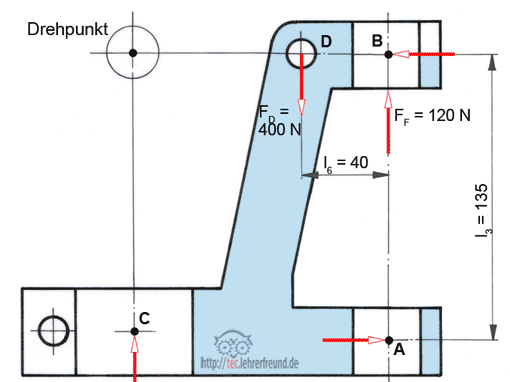
Führungsgabel: 

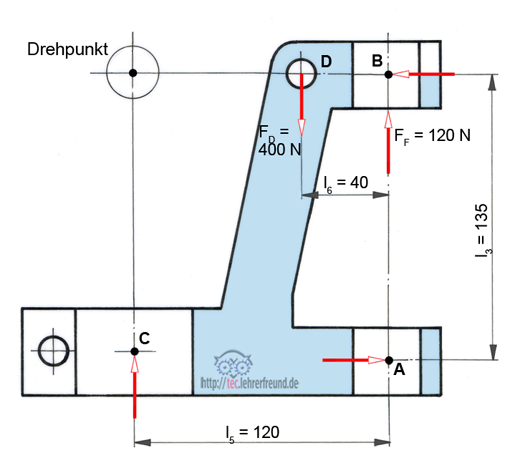
Gegeben: F_D =  400 N (in Aufgabe 1. ist F_D = F_L = 447 N)
Berechnen: F_A, F_B, und F_C (= F_V)

Berechnen: F_A, F_B, und F_C (= F_V) 

Die Wirkungslinien der unbekannten Kräfte F_A und F_B verlaufen waagerecht, weil die Berührungsflächen zwischen Führungssäule und Führungsgabel senkrecht liegen. Dass von der Säule in y-Richtung keine Kräfte übertragen werden, erkennt man daran, dass sich die Führungsgabel auf der Säule ungehindert senkrecht bewegen kann.

Welcher Drehpunkt ist günstig?
Man wählt den Drehpunkt möglichst so, dass er im Schnittpunkt der Wirklinien von unbekannten Kräften liegt. Dieser Punkt wird als Drehpunkt gekennzeichnet. Dann werden Drehmomente der betreffenden Kräfte zu Null, weil die Hebelarme = 0 sind.

Mögliche Schnittpunkte sind: F_C mit F_A oder F_C mit F_B. Wir wählen den Schnittpunkt von F_C mit F_B als Drehpunkt.
Freigemachte Führungsgabel:
- F_D und die Federkraft F_F sind gegeben.
- F_A, F_B und F_C: Die Wirklinien sind gegeben. 

Lösungsvorschlag: 

ΣM_(BC) = 0 = - F_F ∙ l₅ - F_A ∙ l₃ + F_D ∙ l₆  
F_A ∙ l₃ = F_D ∙ l₆ - F_F ∙ l₅ 
F_A = (F_D ∙ l₆ - F_F ∙ l₅) : l₃

F_A = (400 N ∙ 80 mm - 120 N ∙ 120 mm) : 135 mm 

F_A = 130,37 N 

ΣF_x = 0 = - F_B + F_A  –> F_B = F_A =
F_A = 130,37 N

ΣF_y = 0 = F_C - F_D –> F_C =
F_C = 400 N 
_____________________ 

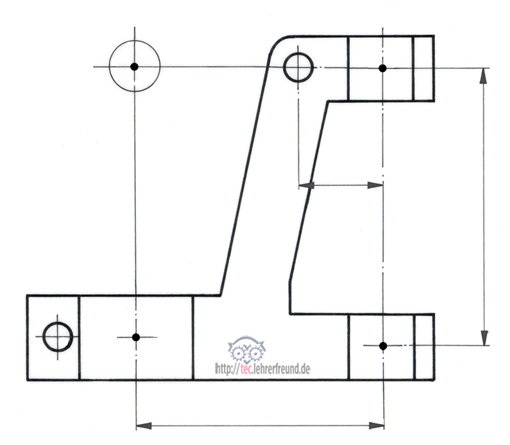
Die Skizzen unten sind für die Verwendung in Arbeitsblättern gedacht.