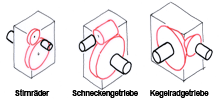
Kegelige Formen bemaßen und berechnen 20.05.2010, 16:24
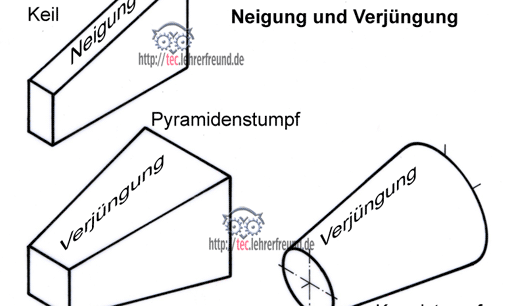
Kegelige Formen stellen in der Bemaßungstechnik einen Spezialfall dar. Bei Zeichnungsangaben ist zwischen den Begriffen »Neigung« und »Verjüngung« zu unterscheiden.
Wie man kegelige Formen bemaßt und berechnet
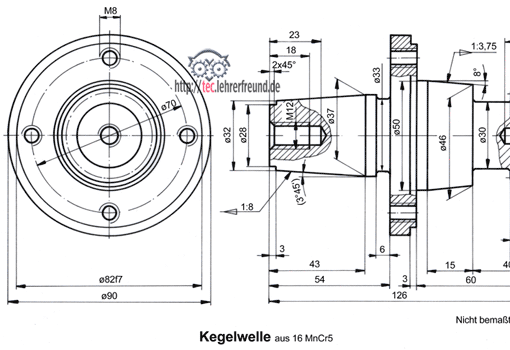
Kegel nach DIN ISO 3040
Bei der Bemaßung von sich verjüngenden Formen unterscheidet die Fachsprache zwischen »Neigung« und »Verjüngung«. Eine Neigung liegt z. B. bei flachen Körpern vor, wenn sie nur eine schräge Fläche besitzen. Von Verjüngung spricht man bei pyramidenförmigen und kegelförmigen Teilen.
Die nachfolgende Beschreibung gilt für Kegel, bei denen an die Genauigkeit der Kegelform höhere Ansprüche gestellt werden. Die Bemaßung von kegeligen Übergängen an Werkstücken, Fasen usw. siehe »Bemaßungsregeln (3)«
Neigung C/2: Man bildet das Verhältnis aus der Differenz H – h und a: Neigung C/2 = (H – h) : a. Die Neigung kann als Verhältniszahl oder in Prozent angegeben werden. Eine praktische Anwendung sind z. B. Keile (DIN 6886): Ihre Neigung beträgt 1:100 = 1%.
Die Neigung ist die halbe Verjüngung.
Bild: Neigung und Verjüngung bei flachen und pyramidenförmigen Teilen
Das Kegel-Symbol ist ein gleichseitiges Dreieck mit 30° und weist in die Richtung der Kegelverjüngung. Es ist auf einer abgewinkelten Hinweislinie über der Kegelmantellinie parallel zur Kegelachse zu zeichnen. Symbole ordnet man vor der Maßzahl an (hier: liegendes Dreieck vor das Kegelverhältnis 1 : 6 setzen).
– Die Kegelverjüngung C: Sie wird entweder als Kegelverhältnis 1 : x oder durch den eingeschlossenen Kegelwinkel α angegeben. Die Verjüngung ist der auf die Kegellänge bezogene Durchmesserunterschied ø D – ø d. Oder:
Das Kegelverhältnis C ist das Verhältnis der Durchmesserdifferenz zur Kegellänge. Kegelverhältnis 1 : 6 würde heißen: Auf 6 mm Kegellänge verjüngt sich der Durchmesser D um 1 mm.
C = (D – d) : L = 1 : 6.
Im Bild verjüngt sich der 90 mm lange Kegelstumpf um 15 mm. D. h. C = 15 : 90 = 1 : 6.
– den Durchmesser an einem ausgewählten Querschnitt, z.B. größter Kegeldurchmesser, oder Durchmesser eines Querschnitts
– das Maß für die Lage des Querschnitts, z. B. Länge des Kegelstumpfes (Maß 100)
– den Einstellwinkel α/2 als eingeklammertes Hilfsmaß für die Fertigung. Zusätzlich können weitere Maße als eingeklammerte Hilfsmaße angegeben werden, z. B. der zweite Durchmesser beim Kegelstumpf.
Die Angabe des Einstellwinkels α/2 ist beim Drehen und Schleifen eine Hilfe für das Einstellen der Maschinen.
Anmerkung:
Es gilt die Bemaßungsregel: Nicht mehr als die unbedingt notwendigen Maße eintragen. Trägt man trotzdem mehr Maße ein, die dann zu einer maßlichen Überbestimmung führen, dann kennzeichnet man diese dadurch, dass man sie als Hilfsmaße in Klammern setzt.
Den Kegelwinkel berechnet man über den Neigungswinkel (= Einstellwinkel) α/2:

Ein bei Werkzeugschäften häufig vorkommender Kegel ist der Morsekegel nach DIN 228. Er wird mit Zahlen 0, 1, 2, 3, 4, 5 und 6 bezeichnet (6 ist der größte Morsekegel). Durch seine schwache Verjüngung (ca. 1 : 20) besitzt er eine starke Selbsthemmung, d. h. er hält beim Arbeiten des Werkzeugs (Bohrer, Reibahle, Fräser usw.) in der Aufnahmebohrung hohen Verdrehmomenten stand.
Berechnungsbeispiele
1. Die Schenkelneigung C/2 eines Profilstahls ist 12%. Berechnen Sie die Neigung als Verhältniszahl.
Lösung:
C/2 = 12% = 12 : 100 = 1 : 8,333
2. Prüfen Sie die Richtigkeit des Einstellwinkels am oben gezeichneten Kegel (D = 45; d = 30; L = 90) nach.
Lösung:
tan α/2 = (D - d) : 2 L = (45mm - 30mm) : (2 ∙ 90mm) = 0,08333 –>
α/2 = 5,0°
3. Der halbe Kegelwinkel α/2 eines Morsekegels 3 ist 1° 26’ 16’‘. Wie groß ist sein Kegelverhältnis C/2?
Lösung:
C/2 = tan α/2;
α/2 = 1° 26’ 16’‘ –> tan 1° 26’ 16’’ = 0,0250992
C/2 = 0,0250992 = 1 : 39,8418 (erhält man über die 1/x-Taste)
C = 2 · 1 : 39,8418
C = 1 : 19,9209
____________________
Das Rechnen mit Winkeln und Zeiten übt der tec.LEHRERFREUND im nächsten Beitrag.