Ich bin Hermann Metz. Als Maschinenbau-Ingenieur (FH) arbeitete ich von 1977 bis 2005 als Fachlehrer an der Gewerbeschule Breisach, wo ich alle gängigen Fächer der Land- und Baumaschinentechnik und der Kraftfahrzeugtechnik unterrichtete. Dabei hatte ich mit Fach- und Meisterschülern zu tun.
Aus meiner Lehrerfahrung habe ich hier Vorlagen für den Technikunterricht zusammengestellt. Sie finden darin methodische und didaktische Anregungen, Folien, Arbeitsblätter usw.Riementrieb Berechnung
Drehzahl, Umfangsgeschwindigkeit, Übersetzungsverhältnis: Was am Riementrieb anschaulich gelehrt und gelernt werden kann, ist die Grundlage für eine Reihe anderer Techniken.
Diesen Beitrag weiterempfehlen
Zu diesem Beitrag
Eingetragen am 24.05.2008, 14:26 Uhr in Technische Mathematik | Geschwindigkeit | Themenschrank | Riementriebe |
25 x kommentiert, 12117 x gelesen in 2012. Diesen Beitrag kommentieren.
So rechnet man‘s - 2. Ausbildungsjahr
Drehzahlen kann man auf verschiedene Arten verändern. Drei häufig verwendete mechanische Systeme dafür sind Antriebe durch Riemen, Ketten und Zahnräder. Von diesen wollen wir uns hier den Riemenbetrieb ansehen.
Antrieb, Abtrieb
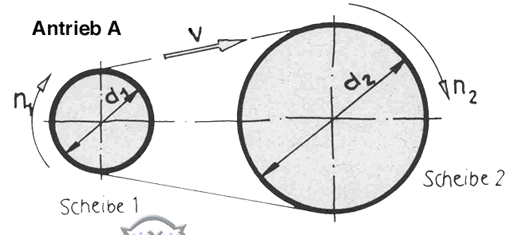
Die Größen, die am Riementrieb rechnerisch von Bedeutung sind, sind die Scheibendurchmesser d1 und d2 und die Drehzahlen n1 und n2 (Zeichnung rechts: Antrieb A). Bei den Fußzahlen (oder »Indizes«) 1 und 2 hat man sich darauf geeinigt, dass 1 immer die Antriebsseite und 2 die Abtriebsseite meint. d1 und n1 sind also der Durchmesser und die Drehzahl der treibenden Scheibe. Dies gilt auch für Ketten- und Zahnräder. Die Indizes 1 und 2 dürfen auf keinen Fall vertauscht werden.
Vergleichen wir Antrieb A und Antrieb B. Wenn die Antriebsdrehzahl in beiden Fällen 1000 1/min wäre: In welche Richtung verändern sich dann die Abtriebsdrehzahlen?
Wenn Sie gefunden haben, dass sich im Fall von Antrieb A die Abtriebszahl verringert (= Übersetzung ins Langsame), im Fall von Antrieb B dagegen vergrößert (= Übersetzung ins Schnelle), dann war Ihre Überlegung richtig.
Rechenformeln
(v = Riemengeschwindigkeit in m/s oder m/min)
Wir müssen in der Lage sein, jeweils eine der erwähnten Größen auszurechnen, also n1 oder n2 oder d1 oder d2. Außerdem benötigen wir in diesen Rechnungen immer wieder das »Übersetzungsverhältnis« i.
Betrachten Sie Antrieb A: Wenn der Riemen läuft, besitzt er zwangsläufig an jeder Stelle dieselbe Geschwindigkeit v. Die Riemengeschwindigkeit v ist also auf Scheibe 1 gleich groß wie auf Scheibe 2:
v1 = v2
Für v können wir aber auch schreiben:
Merksatz:
Ist i > 1, geht die Übersetzung ins Langsame.
Ist i < 1, geht die Übersetzung ins Schnelle.
Riementrieb: Weitere Aufgaben
a) Stellen Sie die Grundformel 1 nach d1, n1, d2 und n2 um. Prüfen Sie Ihre Ergebnisse mit dem Tabellenbuch nach.
b) Antrieb A: d1 = 58 mm; n1 = 3000 1/min; n2 = 750 1/min. Berechnen Sie d2 und i
c) Antrieb B: Die Übersetzung des Riemenantriebs sei 0,8, d1 = 240 mm und n1= 1750 mm. Berechnen Sie d2 und i
Lösungen:
Beispiel aus der Praxis
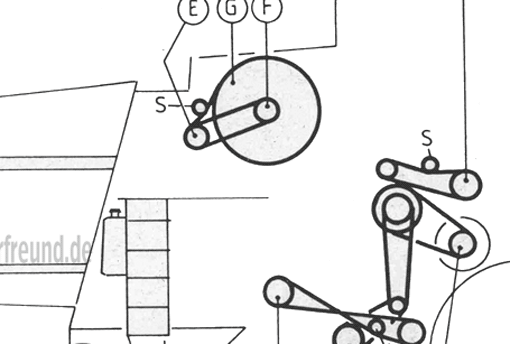
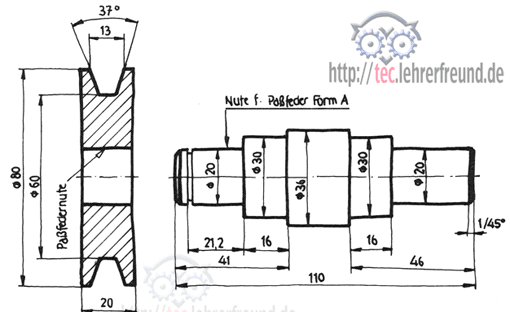
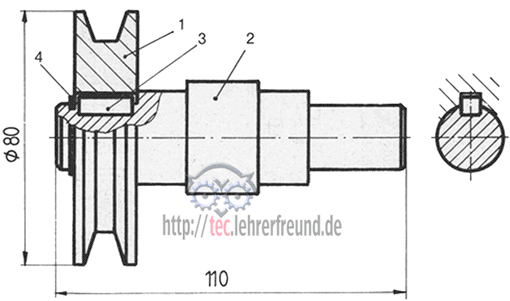
Wir sehen uns ein an einem Motor ausgeführtes Riementrieb-System an. Der Antrieb erfolgt von der Kurbelwelle aus; die untere große Scheibe ist also Nummer 1. Von der Kurbelwellenscheibe, die zwei Rillen besitzt, geht ein Riemen zum Kühlluftgebläse und einer zum Generator. Die technischen Angaben des Antriebs finden Sie in den Bildern. Darin sind die drei Antriebsstränge voneinander getrennt gezeichnet.
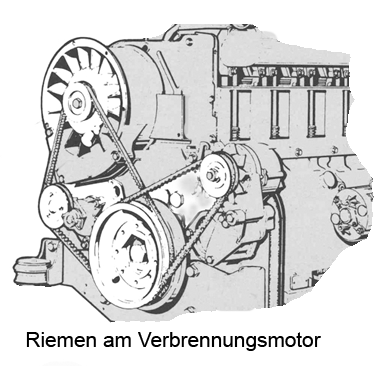
Der Gebläseantrieb enthält eine zusätzliche Spannrolle, mit der sich die Riemenspannung einstellen lässt. Diese hat keinen Einfluss auf das Übersetzungsverhältnis. Falls Ihnen dies nicht sofort einleuchtet, brauchen Sie sich nur vorzustellen, dass die Spannrolle weiter innen sitzt und so den Riemen nur ganz schwach nach links drückt. Für unsere Berechnung können wir davon ausgehen, dass es sich um zwei einfache Riemenübersetzungen handelt (strichpunktierte Linie in der mittleren Skizze).
Aufgaben dazu:
a) Welches Übersetzungsverhältnis liegt im Kühlluftgebläse-Antrieb vor?
b) Welchen Durchmesser besitzt die Gebläsescheibe?
c) Mit welcher Drehzahl läuft die Spannrolle?
d) Welche Laufgeschwindigkeit in m/s erreicht der Riemen?
Für den Generatorantrieb wollen wir etwas Anderes berechnen:
e) Wie groß ist der Achsabstand zwischen Kurbelwellenmitte und Generatormitte?
f) Welche ungefähre Länge besitzt der Keilriemen, wenn die Riemenscheibe auf dem Generator einen Durchmesser von 137 mm hat? (Anmerkung: Die Formel für die exakte Berechnung von Riemenlängen hat es in sich. In Berufsschulen wird sie deshalb ausgespart - daran halten auch wir uns.)
Lösung zu "Riementrieb im Motor"
Gebläseantrieb
Generatorantrieb
(wir schreiben keine Maßeinheiten)
Zum Üben:
So stellt man technische Formeln um
Ergänzung
Kommentar jo
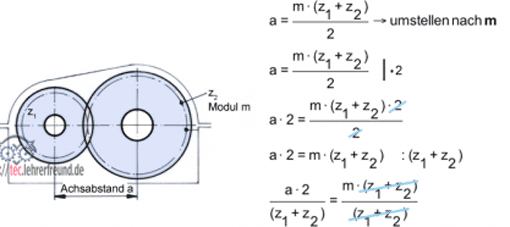
Wir stellen die Formel l = ... nach a (= Achsabstand) um:
Zu diesem Beitrag
Eingetragen am 24.05.2008, 14:26 Uhr in Technische Mathematik | Geschwindigkeit | Themenschrank | Riementriebe |
25 x kommentiert, 12117 x gelesen in 2012. Diesen Beitrag kommentieren.
25 Kommentare von Lehrerfreund/innen
Bei Lösung zu “Riementrieb im Motor”
f) Länge des Keilriemen
Rechnung ist für mich nicht nachvollziehbar. Würde mich über Aufklärung freuen.
Vielen Dank im Voraus.
Hallo Wolfram, Carsten,
Sie haben Recht und ich bitte um Entschuldigung dafür: Mir ist die Spannrolle (ø112) auf die Generatorwelle gerutscht. Der reine Unfug! Die Aufgabe f) ist so nicht lösbar, weil von der Generatorseite zu wenig bekannt ist.
Ich gehe von Ihrem Einverständnis aus, die exakte Riemen(monster)formel nicht zu verwenden. Ich habe mich in f) für eine leichte Textänderung entschieden, die Sie jetzt im Beitrag nachlesen können.
Viele Grüße
tec.LEHRERFREUND
diese rechnung ist totaler mist, unser meister sagt drehzahl brauchen wa nicht
Hallo Werner!
Na, wenn der Meister dat schon sacht,
dann b´hüt di Gott und gute Nacht!
Wusste für den Ausspruch er einen Grund?
Oder is der Mann sonstwie nich gesund?
Gruß
tec. LEHRERFREUND
Ich glaub ich bin mitlerweile zu blöde für
diese Welt.ich komm mit den Formeln nicht klar.
Ich habe eine Drehzahl von 400 u/min bei einer 63mm Riemenscheibe und will auf 600 u/min kommen.welche riemenscheibe muss ich da nehmen?
HILFE
Danke im Vorraus
Hallo Hermann,
in Ihrem Beispiel liegt eine Übersetzung ins Schnelle vor. Die Grundformel heißt
n1 x d1 = n2 x d2
Sie suchen d2: d2 = n1 x d1 : n2
d2 = 400 U/min x 63 mm : 600 U/min =
d2 = 42 mm
Gruß
tec.LEHRERFREUND
Riementrieb Aufgabe b) muss es heißen berechnen Sie d2 und i 
Hallo Jakob,
vielen Dank für den Hinweis. n2 wurde in i abgeändert.
Gruß
tec.LEHRERFREUND
Also die Nährung für x ist wohl etwas sehr stark genähert. Man könnte wenigstens davon ausgehen, dass der Riemen jeweils die Kurbeln zur Hälfte umschlingt und somit über nen Pythagoras und den Durchmessern was nettes konstruieren, oder?
Hallo jo,
falls Sie Aufgabe e) meinen: Die haben wir mit dem Pythagoras gerechnet, weshalb auch ein exaktes Ergebnis herauskommt.
Falls Sie aber Aufgabe f) meinen: Die Riemenlänge ist in der Tat angenähert. Aber lesen Sie bitte auch die Anmerkung: Die Formel für die exakte Berechnung von Riemenlängen hat es in sich. In Berufsschulen wird sie deshalb ausgespart - daran halten auch wir uns.
Gruß
tec.LEHRERFREUND
ich habe da einen Rundungsfehler gefunden und zwar bei der Aufgabe f das endergebnis muss lautten 1519mm.
ansonsten Klasse sache !!
hallo nochmal, ich meinte aufgabe f). ich finde als näherung zweimal den achsabstand zu nehmen doch etas sehr stark vereinfacht. unterrichte selber an ner berufsschule, deshalb ist mir schon klar, dass eine genaue berechnung nicht im sinne des erfinders ist.
mfg
Hallo jo,
jetzt machen wir´s doch einmal genauer. Oben in »Ergänzung, Kommentar jo« habe ich Ihnen die genaue Längenformel aufgeschrieben. Die Näherungsrechnung für das ausgewählte Beispiel führte demnach zu dem fast vernachlässigbaren Fehler von etwa 0,7 Prozent. Sollte man eigentlich springen lassen können, oder?
Gruß
tec. LEHRERFREUND
Scheine leider auch zu blöd für Formeln zu sein :-(( Habe einen Motor,der 2800 Umdrehungen macht,benötige aber nur 1400 Umdrehungen,wie groß müßten dann die Riemenscheiben sein???
Mit freundlichen Grüßen
Andre
Hallo André,
auf dem Motor sitzt die kleinere Scheibe, am Abtrieb die größere. Die Drehzahlen n1 : n2 bilden das Verhältnis 2:1 = 2800 : 1400. Bei den Scheibendurchmessern ist es umgekehrt: d2 : d1 = 2:1. Beispiel: Antrieb d1 = 75 mm, Abtrieb d2 = 150 mm.
Gruß
tec.LEHRERFREUND
Fein, fein, die angegebene exakte Lösung liefert das gleiche Ergebnis wie meine selbsterarbeitete Lösung, also stimmt meine “Hausaufgabe”.
Allerdings habe ich in der Praxis typischerweise eher das umgekehrte Problem: Riemenscheiben und Riemen sind standardisierte Katalogware und ich hätte gerne den richtigen Achsabstand ermittelt.
Seit einiger Zeit versuche ich nun also die exakte Gleichung analytisch geschlossen so umzustellen, daß ich den Achsabstand als Funktion der Scheibendurchmesser (oder -radien) und des Riemenumfangs bekomme. Mittlerweile habe ich schon das gesammelte Wissen der Herren Bronstein, Semendjajew, Musiol und Mühlig über Dreiecke, trigonometrsiche Funktion und wer weiß was noch zu Rate gezogen, und komme zu dem Schluß, daß hier jetzt entweder numerische Verfahren oder Taylor-Reihen angesagt sind, weil in dieser Richtung für das Dreieck eine weitere Angabe fehlt. Andererseits werde ich das Gefühl nicht los etwas übersehen zu haben, vielleicht ein Additionstheorem? Gibt es da möglicherweise noch einen Trick vom Fachmann?
Gruß
René
Hallo René,
es ist eigentlich kein Trick, sondern nur die Umstellung der Formel l = ... nach a = ...
Wir haben das gemacht; Sie finden die Umstellung am Ende des Beitrags »Riementrieb Berechnung«.
Beste Grüße
tec.LEHRERFREUND
Sehr großen Dank für das Umstellen der Gleichung. Ganz offensichtlich ist nun aber ausser den Größen d1, d2 und l (Durchmesser der beiden Riemenscheiben und Umfangslänge des Riemens) auch noch der Winkel alpha vorzugeben. Dummerweise habe ich alpha aber nicht, nur die Bauteile und damit d1, d2 und l; ganz frei wählbar ist alpha aber auch nicht, denn gemäß der Dreiecksgesetze hängt alpha unter anderem auch vom Achsabstand a ab. Und an eben dieser Auflösung (Ersatz von alpha) durch einen Ausdruck mit nur den gegebenen Größen scheitere ich - leider. In meiner resultierenden Gleichung steht alpha, wie schon in Ihrer Formel, direkt als Faktor und später implizit in einem Teilterm ...cos(arcsin(.a..). Dafür bräuchte ich einen Kniff oder ich sollte ich doch schon mal den Rechenknecht warmlaufen lassen?
Grüße und Dank
René
PS: mir ist durchaus klar, daß diese Problemstellung das Niveau der Berufsschule überschreiten könnte - das ist nicht abwertend gemeint!
Hallo René,
der Riemenformel-Gott nimmt, fürchten wir, keine Rücksicht auf Ihre durchaus praktischen Erwägungen. Er will, dass Sie mit dem Umschlingungswinkel alpha leben.
Aber müssen Sie sich wirklich über alpha aufregen? Wir sagen: Nein!
Sie werden ja kaum mit einem Riementrieb zu tun haben, er nicht mit Nachspannmöglichkeiten ausgerüstet ist. Vergessen Sie alpha einfach und nutzen Sie die Spanneinrichtung, um mit Ihren Riemen zurechtzukommen.
Wenn Ihnen das zu rustikal erscheint: Machen Sie eine genaue, maßstäbliche Zeichnung der Ihnen vorliegenden Situation mit d1, d2 und a und messen Sie den Winkel tau heraus, mit dem Sie die Umschlingungswinkel ausrechnen können. Den Rest erledigen Sie mit der Riemenlänge-Formel.
Grüße
tec.LEHRERFREUND
Hallo
ich komme mit meiner rechnerrei nicht weiter,könnt ihr mir helrfen?
Ich habe einen Riementrieb der Motor macht 1430 U/min, die Riemenscheibe n1 ist 120mm groß, Riemenscheibe n2 100mm groß. n2 treibt ein 600mm großes Sägeblatt an.Wie schnell dreht sich das Sägeblatt?
Gruß
Markus
Hallo Markus,
weil das Sägeblatt fest mit der Riemenscheibe 2 verbunden ist, dreht es genau so schnell wie die Riemenscheibe, also mit n2:
n2 = n1 x d1 : d2
n2 = 1430 U/min x 120 mm : 100 mm =
n2 = 1716 U/min.
Gruß
tec.LEHRERFREUND
Prima danke schön!!!
Gruß
Markus
Hallo Gemeinde,
mal als kleiner Tipp, wer eine praxisnahe Berechnung (wer möchte, sogar mit Software) schaut mal bei der Firma Optibelt auf die Hp. Da gibt es Kataloge und Berechnungen on mas.
Grüße von mir hier
wie berechne ich die Umdrehungsgeschwindigkeit einer Keilriemenscheibe. Wenn die Antriebsscheibe einen Durchmesser von 80 mm und eine Umdrehungsgeschwindigkeit von 1000 Upm hat. Und die Abtriebsscheibe 190 mm Durchmesser. Wie hoch ist die Abtriebsumdrehung??
Gruß Willi
Hallo Willi,
die Antriebsscheibe hat den Index 1, die Abtriebsscheibe den Index 2. Sie suchen n2.
Aus der Grundgleichung
d1 x n1 = d2 x n2 (x = Malzeichen) ergibt sich
n2 = d1 x n1 : d2
n2 = 421 U/min
Gruß
tec.LEHRERFREUND
Geben Sie Ihren Kommentar hier ein:
Hinweis: Der Kommentar wird von einem Moderator geprüft.
1756 Einträge, 12437 Kommentare
Seite generiert in 0.5063 Sekunden bei 140 MySQL-Queries
75 Personen online (max. 209 am 18.03.2012)