Fahrrad: Kräfte an der Handbremse 19.01.2012, 15:43

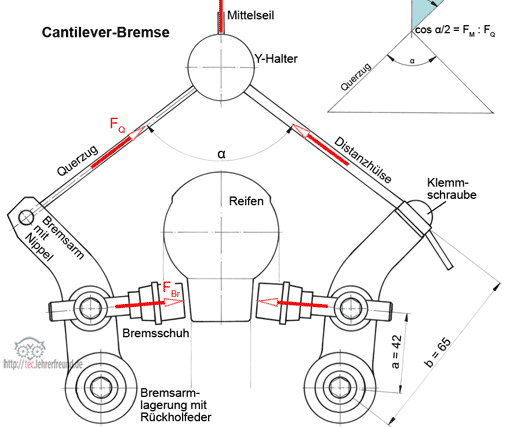
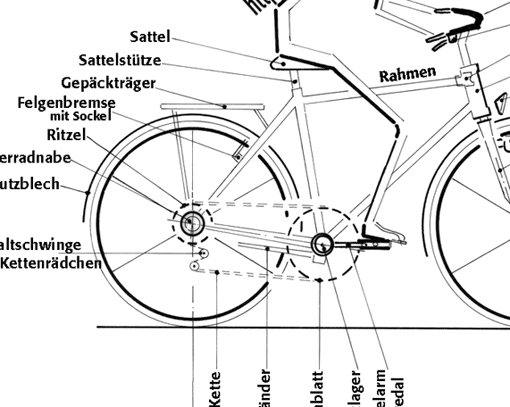
Cantilever ist der englische Begriff für einen einseitigen Hebel. Die Bremsarme von Cantilever-Felgenbremsen sind an Sockeln auf der Fahrradgabel gelagert. Wie wirken die Kräfte an dieser Bremse?

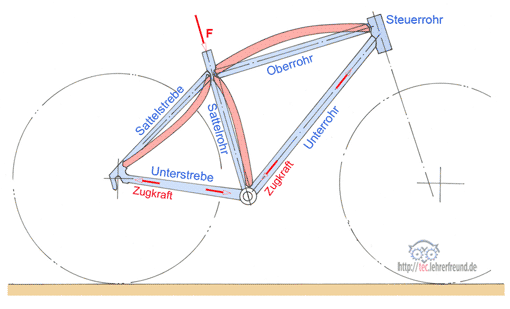
Kräfte an der Fahrrad-Handbremse
Cantileverbremse

Mechanisch betätigte Fahrradbremsen sind
- die Seitenzugbremse
- die Mittelzugbremse
- die Cantileverbremse
- die V-Bremse.

Die hier dargestellte Cantileverbremse hat gegenüber ihren Vorgängerinnen einige Vorteile:
- Sie besitzt ein günstiges Übersetzungsverhältnis am Bremshebel.
- Sie überträgt hohe Bremskräfte auf die Felge.
- Ihre kurzen Hebelarme machen sie verwindungssteif und unempfindlich gegen Verschmutzung. Die Bremsarmlager sind in den an der Vordergabel angeschweißten Sockeln festgeschraubt.
- Cantileverbremsen lassen sich problemlos entspannen, wenn man den Kabelnippel aus dem geschlitzten Ende des Bremsarms herausnimmt.
- Jeder Bremsarm hat eine eigene Rückholfeder. 

Die Bremsarme der Cantileverbremsen werden so auf die Bremssockel montiert, dass die Rückholfeder in einer Bohrung des Sockels verankert werden kann. Das andere Ende der Rückholfeder hat eine Gegenhalterung im Bremsarm. Das Bremsarmlager wird mit einer Schraube am Bremssockel befestigt.

(Cantilever ist ein häufig benutzter englischer Fachbegriff und bedeutet »Ausleger, Kragarm« u. v. Andere) 

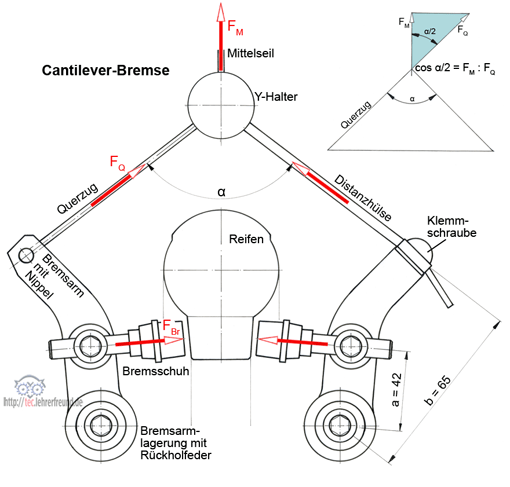
Kräfte an der Cantileverbremse 

Wird auf das Mittelseil die Kraft F_M ausgeübt, dann entstehen in den Querzügen die Kräfte F_Q und die Bremsklötze drücken mit F_Br auf die Felgen. 

1. Bremsarm: Welches Übersetzungsverhältnis hat der Bremsarm grob überschlagen? 
a) 2,5 : 1    b) 2,0 : 1     c) 1,5 : 1    d) 1 : 1? 

Lösungsvorschlag: 

1. Richtig ist c)

2. Bei gegebener Mittelseilkraft F_M soll die Kraft F_Br ermittelt werden, die von den Bremsbelägen auf die Felge ausgeübt wird. 

Gegeben: F_M = 230 N; Spreizwinkel α = 90°; α/2 = 45° 
Gesucht: F_Br

Lösungsvorschlag: 

cos α/2 = F_M : F_Q ––> F_Q = F_M : cos α/2 =

F_Q = 230 N : 0,707 = 325,3 N

Hebelgesetz 

Linker Bremsarm: M_li = M_re

F_Br • a = F_Q • b 

F_Br = F_Q • b : a = 325,3 N • 65 mm : 42 mm

F_Br = 503,5 N 

3. Es soll zeichnerisch festgestellt werden, wie sich beim Bremsen die Querzugkräfte F_Q bei unterschiedlichen Spreizwinkeln α₁ und α₂ verhalten.  
Gegeben:
F_M1 = F_M2 = 500 N;
α₁ = 100°; α₂ = 80°
Gesucht: F_Q1 und F_Q2 

Lösungsvorschlag:  

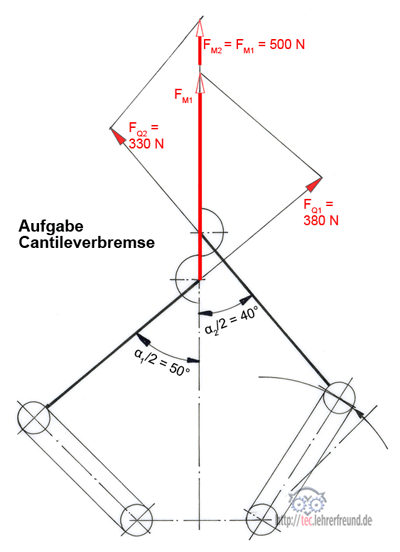
Je kleiner der Gesamt-Spreizwinkel α wird, desto kleiner wird die Querzugkraft.

4. (Schwierig!)
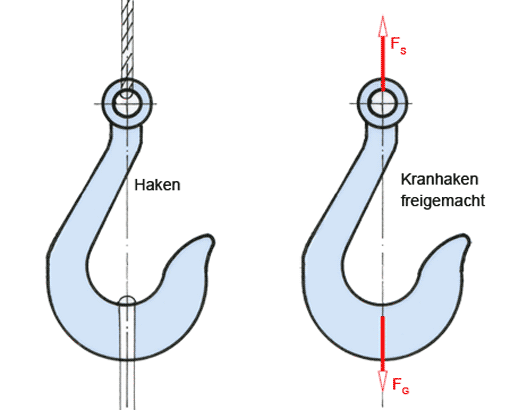
a) Machen Sie den linken Bremsarm frei. Die Federrückholkraft soll nicht berücksichtigt werden. 

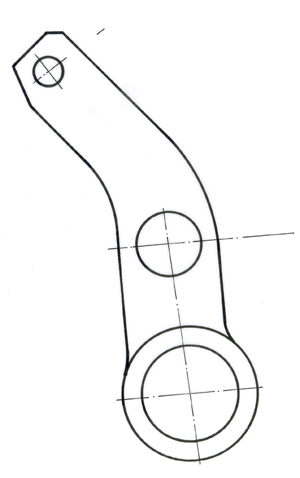
b) Zeichnerisch: Bei gegebener Bremsnormalkraft F_Br = 500 N soll die Querzugkraft F_Q und die Bremsarm-Lagerkraft ermittelt werden.

Lösungsvorschlag: 

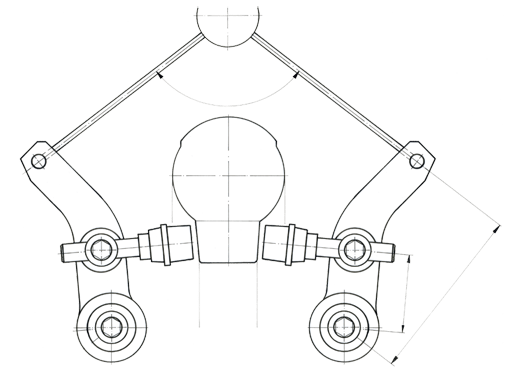
a) Bremsarm freigemacht 

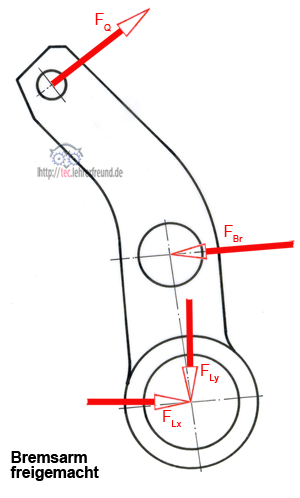
b)

Die Skizze unten ist für die Verwendung in Arbeitsblättern gedacht.