Beispiele und Vergleiche im Freihandversuch 07.06.2008, 17:33
Einem technischen Unterricht ohne Freihandversuche fehlt viel. Sie finden hier einige Beispiele für Freihandversuche.
Zur (schwierigen) BERNOULLI-Gleichung.
 Venturi und Bernoulli fanden heraus, dass in strömenden Gasen oder Flüssigkeiten ein Geschwindigkeitsanstieg einen Druckabfall zur Folge hat. Erfahrungsgemäß ist der Schüler davon überzeugt, das Gegenteil sei der Fall, wenn also etwa eine Flüssigkeit in einem Rohr schneller strömt, müsse mit der größeren Geschwindigkeit v auch der Druck p zunehmen. Wir können unserem Schüler mit Engelszungen erklären, dass der Druck abnimmt: Er wird es uns niemals glauben.
Venturi und Bernoulli fanden heraus, dass in strömenden Gasen oder Flüssigkeiten ein Geschwindigkeitsanstieg einen Druckabfall zur Folge hat. Erfahrungsgemäß ist der Schüler davon überzeugt, das Gegenteil sei der Fall, wenn also etwa eine Flüssigkeit in einem Rohr schneller strömt, müsse mit der größeren Geschwindigkeit v auch der Druck p zunehmen. Wir können unserem Schüler mit Engelszungen erklären, dass der Druck abnimmt: Er wird es uns niemals glauben.
Also beweisen wir es ihm mit einem einfachen Beispiel, einem Freihandversuch: Wir nehmen zwei DIN A4-Blätter, lassen sie mit 3 bis 4 cm Abstand herunterhängen, Skizze a), und blasen dann durch, Skizze b). Beim Blasen zieht es die Blätter zueinander hin:

Damit dürfte für alle Zeiten niemand mehr ein Problem damit haben,
- dass am Flugzeugflügel dort, wo die Luft schneller strömt (nämlich oben) der Druck abfällt und deshalb das Flugzeug angehoben wird und fliegt. (Diese Erklärung des Auftriebs ist heute aber nur noch bedingt richtig), oder:
- dass im Schweißbrenner der schnellere Sauerstoff das an ihn herangeführte Brenngas Azetylen nicht wegdrückt, sondern ansaugt (Injektionsprinzip), oder:
- dass der Druckabfall in Hydrauliksystemen dafür genutzt werden kann, Funktionen zu steuern.
Ein solcher allereinfachster Freihandversuch liefert natürlich kein Messergebnis, sondern zeigt nur die Erscheinung. Er weckt das Interesse des Schülers und macht ihn dadurch aufmerksam. Was will man im Unterricht mehr?
Wir basteln ein Reibradmodell
Weil nicht jeder Feihandversuch ist mit so geringem Aufwand möglich ist, wird manchmal die Bastelbereitschaft des Lehrers stark herausgefordert: Etwa für den Nachweis, dass Räder mit derselben Umfangsgeschwindigkeit laufen, sobald sie als Reibräder, durch Riemen oder Zähne verbunden sind, geht es kaum ohne Werkbank, Bohrmaschine und Sperrholz ab.
Das Modell besteht aus 3 Reibrädern - einfache Sperrholzrädchen, deren beide äußeren über Hebel an das mittlere Rad gedrückt werden. Die Hebel sind auf einer Grundplatte fixiert.
Das Versuchsziel: Klären, dass alle drei Räder mit derselben Geschwindigkeit laufen. Wäre es nicht so, müsste das schneller laufende Rad das langsamere überholen.
Anwendung hier: Berechnungen zum Riementrieb
Wo liegen die Grenzen des Freihandversuchs?
Es ist überhaupt die Frage, wann die Grenze des Freihandversuchs erreicht ist. Sobald kompliziertere Einrichtungen erforderlich sind - dazu könnte man etwa den einfachen Versuch mit einer Federwaage zählen, dessen man sich bedient, um die Federkennlinie zu ermitteln -, wird man nicht mehr von einem Freihandversuch sprechen. In einigen Bereichen wie der Elektrik/Elektronik oder der Hydraulik kann man nur vereinzelt auf Freihandversuche zurückgreifen. So ließe sich der Stromlaufplan z. B. nur schwer ohne Steckbrett, originale elektrische Bauteile und Multimeter darstellen. Ähnlich: Übung zum Ohmschen Gesetz.
 Schwieriges mit Einfachem vergleichen: Synchronisierung von Schaltgetrieben
Schwieriges mit Einfachem vergleichen: Synchronisierung von Schaltgetrieben
Schwieriges mit Einfachem vergleichen (um das Schwierige zu begreifen) kann ebenfalls mit einem Freihandversuch bewerkstelligt werden; es gibt auch verbal unterstützte Möglichkeiten. Ein Beispiel dafür wäre der Vorgang beim Synchronisieren in Schaltgetrieben, das man mit der Stabübergabe beim Staffellauf vergleicht.
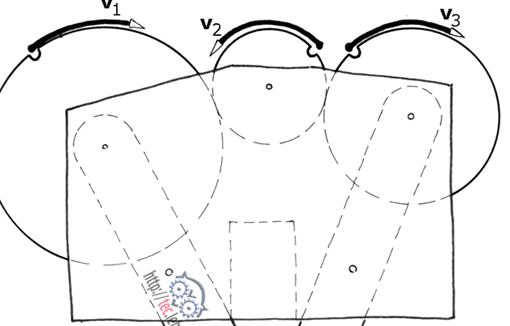
Das Problem, mit der stark vereinfachten Freihandskizze unten erläutert:
Ein Auto fährt im 1. Gang: Rad 1 treibt Rad 2 an. Jetzt soll der 2. Gang geschaltet werden, Rad 3 steht aber. Wie lässt sich das laufende Rad 1, ohne die Zähne zu beschädigen, ins stehende Rad 3 schieben?
Lösung: 3 muss zuerst auf die Drehzahl von 1 gebracht, d. h. »synchronisiert« werden.
Der Vergleich dazu:
»Das Synchronisieren lässt sich mit dem Stabwechsel beim Staffellauf vergleichen. Würde der den Stab übernehmende Läufer den Übergebenden im Stehen erwarten, entstünde eine Stockung, ein Zeitverlust. Deshalb setzt sich der 2. Läufer schon früher in Bewegung, damit er bei der Stabübergabe etwa die gleiche Geschwindigkeit hat wie der Ankommende.
Ähnlich funktioniert das Schalten der Zahnräder von einem Gang in den andern.«
Siehe auch: Der Bagger: Wohin fließt das Öl?
Klarheit durch Folienschieben
In Hydraulikschaltungen ist das Wegeventil ein Herzstück. Es zeigt dem Öl, wohin die Reise geht. An das Vorstellungsvermögen des Schülers stellt es einige Ansprüche. Deshalb darf der Lehrer froh darüber sein, dass kein Modell über die Funktion dieses Ventils billiger und schneller aufklärt als eine simple Folie.
Die Folie besteht aus drei Teilen: aus dem Ventil selbst in Normdarstellung, dem Anschluss zur Pumpe und zum Tank, und dem Anschluss zum Arbeitszylinder. Zwischen diesen beiden Teilen schieben wir das Ventil - hier ein 4/3-Wegeventil - hin und her, so dass kein Zweifel über die Funktion jeder einzelnen Schaltstellung bleibt. In Wirklichkeit wird natürlich nicht ganze Ventil hin und her geschoben, sondern nur der innen liegende und symbolisch dargestellte Steuerkolben.
Gedankenversuch: Geschwindigkeit und Drehzahl der Erde
Wo sich in Maschinen etwas dreht, ist die Versuchung oft groß, die beiden Größen Drehzahl und Geschwindigkeit (Schnittgeschwindigkeit, Umfangsgeschwindigkeit, Riemengeschwindigkeit usw.) in einen Topf zu werfen. Um der Verwirrung ein Ende zu bereiten, greifen wir zu einem drastischen Vergleich: zur sich drehenden Erdkugel. Drehzahl und Umfangsgeschwindigkeit der Erde werden mit den Schülern erarbeitet. Das könnte so ablaufen:
L: Die Erde dreht sich und wir drehen uns mit. Mit welcher Geschwindigkeit drehen wir uns denn?
Sch: Die Sch schätzen meistens und finden schließlich 100 oder 200 km/h schon einen hohen Wert.
L: Können wir das berechnen?
Sch: Vielleicht fällt dem Einen oder Anderen ein: Die Erde dreht sich 1 Mal pro 24 Stunden um ihre Achse.
L: Zeichnet die Erdkugel an die Tafel/auf die Folie und schreibt die genannten Werte dazu. Wie viele Kilometer legen wir in diesen 24 Stunden zurück?
Sch: Meistens großes Rätselraten, aber auf irgend eine Weise müssen 40 000 km herauskommen, die ebenfalls zur Skizze geschrieben werden.
(Hier könnte man die Sch - um die Frage abzurunden - die Richtung anzeigen lassen, in der wir »fahren«. Große Unsicherheit!)
L: Wie hoch ist also unsere Geschwindigkeit?
Sch: 40 000 km : 24 h = 1667 km/h.
L: Lässt die dazu gehörige Formel v = s : t anschreiben.
Die Enttäuschung darüber, dass wir in unserem Klassenzimmer in Deutschland weniger Weg machen (Punkt D) und damit mit einer geringeren Geschwindigkeit fahren, wird auszuhalten sein. Die beiden sich eindrücklich voneinander unterscheidenden Zahlenwerte für v (1667 km/h) und n (1 Umdrehung/Tag = 0,0007 U/min) müssen am Ende dick an der Tafel stehen.
Zu der sehr kleinen und damit fast wieder nicht vorstellbaren Drehzahl könnten Sie noch fragen, ob man sie irgendwo beobachten kann. Sie würden in einer bestimmt fruchtbaren Debatte auf den Stundenzeiger einer Turmuhr kommen, der aber die doppelte Drehzahl macht. Auch das Wandern des Schattens wir oft genannt.
Zu Umfangsgeschwindigkeit und Drehzahl siehe auch: Riementrieb Berechnung
_____________________________
_____________________________
Anmerkung: Die sich an diese Reihe anschließenden Themen in Technologie, Zeichnen und Rechnen werden wir kontinuierlich ins Web stellen.